八年级数学数据的分析单元练习（二）（北师版）-八年级试卷-众享学科测评

八年级数学数据的分析单元练习（二）（北师版）

满分120分答题时间100分钟

已经有9位用户完成了练习

单选题(本大题共小题，共分)

1.(本小题3分) 数据a，1，2，3，b的平均数为2，则数据a，b的平均数是( )

2.(本小题3分) 已知，，…，的平均数为a，，，…，的平均数为b，则，，…，的平均数为( )

3.(本小题3分) 某班班长统计去年1～8月“书香校园”活动中全班同学的课外阅读数量（单位：本），绘制了如图所示的折线统计图，下列说法正确的是( )

4.(本小题3分) （2021山西）每天登录“学习强国”App进行学习，在获得积分的同时，还可获得“点点通”附加奖励，李老师最近一周每日“点点通”收入明细如表，则这组数据的中位数和众数分别是( )

5.(本小题3分) 5个整数从小到大排列，其中位数是4，如果这组数据的唯一众数是6，那么这5个整数最大的和可能是( )

6.(本小题3分) 在方差的计算公式中，数字10和20分别表示的意义可以是( )

7.(本小题3分) （2021福建）某校为推荐一项作品参加“科技创新”比赛，对甲、乙、丙、丁四项候选作品进行量化评分，具体成绩（百分制）如表： 如果按照创新性占60%，实用性占40%计算总成绩，并根据总成绩择优推荐，那么应推荐的作品是( )

8.(本小题3分) 已知5个正数a₁，a₂，a₃，a₄，a₅的平均数是a，且a₁>a₂>a₃>a₄>a₅，则数据a₁，a₂，a₃，0，a₄，a₅的平均数和中位数是( )

9.(本小题3分) 某校八年级有13名同学参加百米竞赛，预赛成绩各不相同，要取前6名参加决赛，小明已经知道了自己的成绩，他想知道自己能否进入决赛，还需要知道这13名同学成绩的( )

10.(本小题3分) 下列说法：①一组数据的众数只有一个；②样本的方差越小，波动性越小，说明样本稳定性越好；③一组数据的中位数一定是这组数据中的某一数据；④数据：1，1，3，1，1，2的众数为4；⑤一组数据的方差一定是正数．其中正确的说法有( )

填空题(本大题共小题，共分)

11.(本小题3分) 8名学生在一次数学测试中的成绩为80，82，79，69，74，78，73，81，则这组数据的平均数是____．

12.(本小题3分) （2021武汉）我国是一个人口资源大国．第七次全国人口普查结果显示，北京等五大城市的常住人口数如下表，这组数据的中位数是____．

13.(本小题3分) （2021杭州）现有甲、乙两种糖果的单价与千克数如下表所示． 将这2千克甲种糖果和3千克乙种糖果混合成5千克什锦糖果，若商家用加权平均数来确定什锦糖果的单价，则这5千克什锦糖果的单价为____元/千克．

14.(本小题3分) （2021河南）某外贸公司要出口一批规格为200克/盒的红枣，现有甲、乙两个厂家提供货源，他们的价格相同，品质也相近．质检员从两厂产品中各随机抽取15盒进行检测，测得它们的平均质量均为200克，每盒红枣的质量如图所示，则产品更符合规格要求的厂家是____（填“甲”或“乙”）．

15.(本小题3分) 已知数据x₁，x₂，…，x_n的方差是0.1，则4x₁-2，4x₂-2，…，4x_n-2的方差为____．

解答题(本大题共小题，共分)

16.(本小题7分) 某校八年级有5个班，有一次数学知识竞赛中，各班平均成绩分别为=70，=71，=75，=69，=72；有一位同学这样计算这次竞赛年级的平均成绩：； 你同意他的算法吗？若同意，请说明这种算法的正确性；若不同意，请说明理由，并说明在什么情况下这种算法是合理的．

17.(本小题8分) （2021天津）某社区为了增强居民节约用水的意识，随机调查了部分家庭一年的月均用水量（单位：t）．根据调查结果，绘制出如下的统计图1和图2． 请根据相关信息，解答下列问题： （1）本次接受调查的家庭个数为，图1中m的值为； （2）求统计的这组月均用水量数据的平均数、众数和中位数．

18.(本小题8分) 某乡镇企业生产部有技术工人15人，生产部为了合理制定产品的每月生产定额，统计了15人某月的加工零件个数如下： （1）写出这15人该月加工零件数的平均数、中位数和众数． （2）生产部负责人要定出合理的每人每月生产定额，你认为应该定为多少件合适？

19.(本小题8分) 在一次男子马拉松长跑比赛中，随机抽得12名选手所用的时间（单位：分钟）得到如下样本数据：140，146，143，175，125，164，134，155，152，168，162，148． （1）计算该样本数据的中位数和平均数； （2）如果一名选手的成绩是147分钟，请你依据样本数据的中位数，推断他的成绩如何？

20.(本小题10分) 下表是某校九年级（1）班20名学生某次数学测验的成绩统计表： （1）若这20名学生成绩的平均分数为82分，求x和y的值； （2）在（1）的条件下，设这20名学生本次测验成绩的众数为a，中位数为b，求a，b的值．

21.(本小题10分) 某商场服装部为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励，为了确定一个适当的月销售目标，商场服装部统计了每位营业员在某月的销售额（单位：万元），数据如下： 17，18，16，13，24，15，28，26，18，19， 22，17，16，19，32，30，16，14，15，26， 15，32，23，17，15，15，28，28，16，19． 对这30个数据按组距3进行分组，并整理、描述和分析如下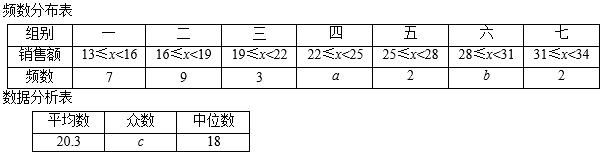： 请根据以上信息解答下列问题： （1）填空：a= ，b= ，c= ； （2）若将月销售额不低于25万元确定为销售目标，则有位营业员获得奖励； （3）若想让一半左右的营业员都能达到销售目标，你认为月销售额定为多少合适？说明理由．

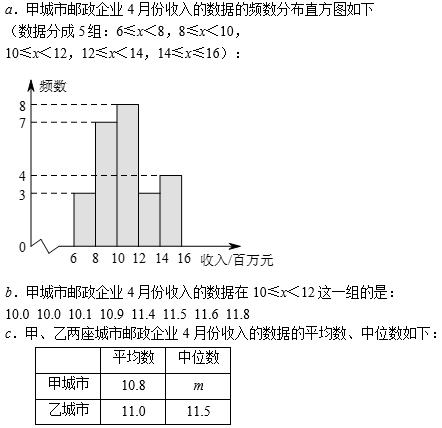
22.(本小题12分) （2021北京）为了解甲、乙两座城市的邮政企业4月份收入的情况，从这两座城市的邮政企业中，各随机抽取了25家邮政企业，获得了它们4月份收入（单位：百万元）的数据，并对数据进行整理、描述和分析．下面给出了部分信息． 根据以上信息，回答下列问题： （1）写出表中m的值； （2）在甲城市抽取的邮政企业中，记4月份收入高于它们的平均收入的邮政企业的个数为p₁．在乙城市抽取的邮政企业中，记4月份收入高于它们的平均收入的邮政企业的个数为p₂．比较p₁，p₂的大小，并说明理由； （3）若乙城市共有200家邮政企业，估计乙城市的邮政企业4月份的总收入（直接写出结果）．

23.(本小题12分) 为积极响应“弘扬传统文化”的号召，某学校倡导全校1 200名学生进行经典诗词诵背活动，并在活动之后举办经典诗词大赛，为了解本次系列活动的持续效果，学校团委在活动启动之初，随机抽取部分学生调查“一周诗词诵背数量”，根据调查结果绘制成的统计图如图所示． 请根据调查的信息分析： （1）把图中条形统计图补充完整，并求活动启动之初学生“一周诗词诵背数量”的中位数； （2）估计大赛后一个月该校学生一周诗词诵背6首（含6首）以上的人数； （3）选择适当的统计量，从两个不同的角度分析两次调查的相关数据，评价该校经典诗词诵背系列活动的效果．