九年级数学锐角三角函数单元练习（二）（人教版）-九年级试卷-众享学科测评

九年级数学锐角三角函数单元练习（二）（人教版）

满分120分答题时间100分钟

已经有0位用户完成了练习

单选题(本大题共小题，共分)

1.(本小题3分) 若∠A，∠B均为锐角，且sinA=，cosB=，则( )

2.(本小题3分) 如图，点A为∠α边上的任意一点，作AC⊥BC于点C，CD⊥AB于点D，下列用线段比表示cosα的值，错误的是( )

3.(本小题3分) 在Rt△ABC中，∠C=90°，在下列条件中不能解直角三角形的是( )

4.(本小题3分) 如果某人沿坡度为3:4的斜坡前进10 m，那么他所在的位置比原来的位置升高了( )

5.(本小题3分) （2021丹东）如图，在矩形ABCD中，连接BD，将△BCD沿对角线BD折叠得到△BDE，BE交AD于点O，BE恰好平分∠ABD．若AB=，则点O到BD的距离为( )

6.(本小题3分) 在Rt△ABC中，∠C=90°，∠A的对边为a，∠B的对边为b，且满足a²-ab-b²=0，则tanA=( )

7.(本小题3分) （2021遵义）如图，点C是以点O为圆心，AB为直径的半圆上一点，连接AC，BC，OC，若AC=4，BC=3，则sin∠BOC的值是( )

8.(本小题3分) 某地下车库出口处安装了“两段式栏杆”，如图1所示，点A是栏杆转动的支点，点E是栏杆两段的联结点．当车辆经过时，栏杆AEF最多只能升起到如图2所示的位置，其示意图如图3所示（栏杆宽度忽略不计），其中AB⊥BC，EF∥BC，∠AEF=143°，AB=AE=1.2米，那么适合该地下车库的车辆限高标志牌为( )（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

9.(本小题3分) （2021宜宾）如图，在△ABC中，点O是角平分线AD，BE的交点，若AB=AC=10，BC=12，则tan∠OBD的值是( )

10.(本小题3分) 如图，∠EFG=90°，EF=10，OG=17，cos∠FGO=，则点F的坐标是( )

填空题(本大题共小题，共分)

11.(本小题3分) 在平面直角坐标系xOy中有一点A(3，4)，如果OA与x轴正半轴的夹角为α，那么 sinα=____．

12.(本小题3分) （2021绥化）边长为4cm的正六边形，它的外接圆与内切圆半径的比值是____．

13.(本小题3分) 某次台风来袭时，一棵大树树干AB（假定树干AB垂直于地面）被刮倾斜15°后折断倒在地上，树的顶部恰好接触到地面D（如图所示），量得树干的倾斜角为∠BAC=15°，大树被折断部分和地面所成的角∠ADC=60°，AD=4米，则这棵大树AB原来的高度是____米．

14.(本小题3分) 如图，AB为⊙O的直径，D为AB上一点，且AB=5AD，CD⊥AB，垂足为D，C在圆上，设∠COD=α，则sin=____．

15.(本小题3分) （2021绍兴）已知△ABC与△ABD在同一平面内，点C，D不重合，∠ABC=∠ABD=30°，AB=4，AC=AD=，则CD的长为____．

解答题(本大题共小题，共分)

16.(本小题8分) 求下列各式的值： （1）； （2）．

17.(本小题9分) 在△ABC中，已知∠C=90°，b+c=30，∠A-∠B=30°．解这个直角三角形．

18.(本小题9分) 如图，某公园内有座桥，桥的高度是5米，CB⊥DB，坡面AC的倾斜角为45°，为方便老人过桥，市政部门决定降低坡度，使新坡面DC的坡度为i=1:．若新坡角外需留下2米宽的人行道，问离原坡角（A点处）6米的一棵树是否需要移栽？（参考数据：≈1.414，≈1.732）

19.(本小题9分) （2021湘西州）如图，AB为⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D． （1）求证：AC平分∠DAB； （2）若AD=8，tan∠CAB=，求边AC及AB的长．

20.(本小题9分) 阅读下列材料： 题目：如图1，在△ABC中，已知∠A（∠A<45°），∠C=90°，AB=1，请用sinA，cosA表示sin2A． 解：如图2，作AB边上的中线CE，CD⊥AB于D， 则CE=AB=，∠CED=2∠A，CD=ACsinA，AC=ABcosA=cosA 在Rt△CED中，sin2A=sin∠CED==2ACsinA=2cosAsinA 根据以上阅读，请解决下列问题： （1）如图3，在△ABC中，∠C=90°，BC=1，AB=3，求sinA，sin2A的值； （2）上面阅读材料中，题目条件不变，请用sinA或cosA表示cos2A．

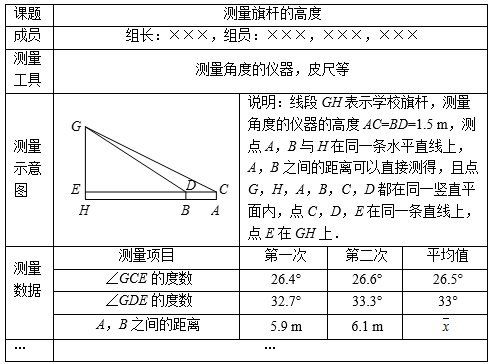
21.(本小题10分) 某校“趣味数学”社团开展了测量本校旗杆高度的实践活动．“综合与实践”小组制订了测量方案，并完成了实地测量．他们在该旗杆底部所在的平地上，选取两个不同测点，分别测量了该旗杆顶端的仰角以及这两个测点之间的距离．为了减小测量误差，该小组在测量仰角的度数以及两个测点之间的距离时，都分别测量了两次并取它们的平均值作为测量结果，测量数据如下表（不完整）． 任务一：两次测量A，B之间的距离的平均值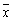= m． 任务二：根据以上测量结果，请你帮助该“综合与实践”小组求出学校旗杆GH的高度．（参考数据：sin26.5°≈0.45，cos26.5°≈0.89，tan26.5°≈0.50，sin33°≈0.54，cos33°≈0.84，tan33°≈0.65） 任务三：该“综合与实践”小组在制定方案时，讨论过“利用物体在阳光下的影子测量旗杆的高度”的方案，但未被采纳．你认为其原因可能是什么？（写出一条即可）

22.(本小题10分) （2021荆门）某海域有一小岛P，在以P为圆心，半径r为海里的圆形海域内有暗礁．一海监船自西向东航行，它在A处测得小岛P位于北偏东60°的方向上，当海监船行驶海里后到达B处，此时观测小岛P位于B处北偏东45°方向上． （1）求A，P之间的距离AP； （2）若海监船由B处继续向东航行是否有触礁危险？请说明理由．如果有触礁危险，那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域？

23.(本小题11分) 均衡化验收以来，乐陵每个学校都高楼林立，校园环境美如画，软件、硬件等设施齐全，小明想要测量学校食堂和食堂正前方一棵树的高度，他从食堂楼底M处出发，向前走6米到达A处，测得树顶端E的仰角为30°，他又继续走下台阶到达C处，测得树的顶端的仰角是60°，再继续向前走到大树底D处，测得食堂楼顶N的仰角为45°，已知A点离地面的高度AB=4米，∠BCA=30°，且B，C，D三点在同一直线上． （1）求树DE的高度； （2）求食堂MN的高度．