七年级数学上学期期末综合练习(二)(北师版)
满分100分 答题时间90分钟
已经有1位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
22.(本小题10分)
探索新知:
如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
(1)一个角的平分线 这个角的“巧分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=α,且射线PQ是∠MPN的“巧分线”,则∠MPQ= ;(用含α的代数式表示)
深入研究:
(3)如图2,若∠MPN=60°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成180°时停止旋转,旋转的时间为t秒.若射线PM同时绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止,请求出当射线PQ是∠MPN的“巧分线”时t的值.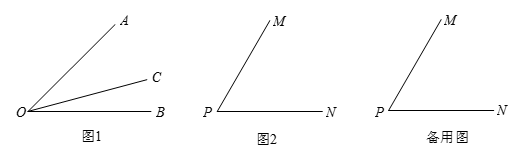
核心考点: 列代数式 解一元一次方程 角平分线的定义 角的运算