八年级数学上学期期末综合练习(一)(人教版)
满分120分 答题时间100分钟
已经有4位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
23.(本小题11分)
数学课上,张老师出示了如下题目.
如图,在△ABC中,∠A=90°,AB=AC,点D为BC的中点,点E和点F分别是边AB和AC上的点,且始终满足DE⊥DF,试确定DE与DF的大小关系.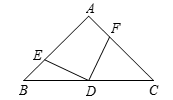
小明与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
如图1,若点E与点A重合时,点F与点C重合,容易得到DE与DF的大小关系.请你直接写出结论:DE DF(填“>”,“<”或“=”).
(2)特例启发,解答题目
如图2,若点E不与点A重合时,DE与DF的大小关系是:DE DF(填“>”,“<”或“=”).理由如下:连接AD.(请你完成剩下的解答过程)
(3)拓展结论,设计新题
在△ABC中,∠A=90°,AB=AC,点D为BC的中点,点E和点F分别是直线AB和直线AC上的点,且始终满足DE⊥DF,若AB=AC=1,BE=2,求CF的长.(请你直接写出结果)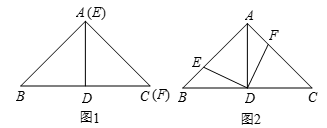
核心考点: 等腰三角形 类比探究 全等三角形的判定及性质














