八年级数学上学期期末综合练习（二）（北师版）-八年级试卷-众享学科测评

八年级数学上学期期末综合练习（二）（北师版）

满分120分答题时间100分钟

已经有73位用户完成了练习

单选题(本大题共小题，共分)

1.(本小题3分) 下列二次根式中，最简二次根式是( )

2.(本小题3分) 下列为勾股数的是( )

3.(本小题3分) 如图，将直尺与含30°角的三角尺摆放在一起，若∠1=20°，则∠2的度数是( )

4.(本小题3分) 下列命题中，假命题有( ) ①两条平行直线被第三条直线所截，内错角相等；②两边分别相等且其中一组等边的对角也相等的两个三角形全等；③三角形的一个外角大于任何一个内角；④如果a²=b²，那么a=b；⑤无限小数是无理数．

5.(本小题3分) 在平面直角坐标系中，点A的坐标为(-2，-3)，线段AB∥x轴，AB=4，则点B的坐标为( )

6.(本小题3分) 已知点(-6，y₁)，(3，y₂)都在直线y=-2x+5上，则y₁与y₂的大小关系是( )

7.(本小题3分) 面试时，某人的基本知识、表达能力、工作态度的得分分别是90分，80分，85分，若依次按20%，40%，40%的比例确定成绩，则这个人的面试成绩是( )

8.(本小题3分) 学完“里程碑上的数”之后有这样一个问题：“小明家离学校1 000米，其中有一段为上坡路，另一段为下坡路．他跑步去学校共用时18分钟，已知小明上坡的平均速度为30米/分，下坡的平均速度为80米/分，小明上坡和下坡各用了多长时间？”小亮同学设出未知数x，y后列出了方程组：，小颖也设出未知数x，y后却列了和小亮不同方程组：，则横线上应填的方程是( )

9.(本小题3分) 如图，函数y=ax+b和的图象交于点P，则根据图象可得，关于x，y的二元一次方程组的解是( )

10.(本小题3分) 如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第一次从原点O运动到点P₁(1，1)，第二次运动到点P₂(2，0)，第三次运动到点P₃(3，-2)，…，按这样的运动规律，第2021次运动后，点P₂₀₂₁的纵坐标是( )

填空题(本大题共小题，共分)

11.(本小题3分) 计算：____．

12.(本小题3分) 当k＞0时，一次函数y=kx+19的图象不经过第____象限．

13.(本小题3分) 若方程x-y=-1的一个解与方程组的解相同，则k的值为____．

14.(本小题3分) 如图，圆柱形容器高为18 cm，底面周长为24 cm，在杯内壁离杯底4 cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2 cm与蜂蜜相对的点A处，则蚂蚁从外壁A到达内壁B处的最短距离为____．

15.(本小题3分) 如图，在平面直角坐标系中，已知直线与x轴、y轴分别交于A，B两点，点C是y轴上一点，把坐标平面沿直线AC折叠，使点B刚好落在x轴上，则点C的坐标是____．

解答题(本大题共小题，共分)

16.(本小题8分) 计算： （1）；（2）．

17.(本小题8分) 解方程组： （1）；（2）．

18.(本小题9分) 在推进嘉兴市城乡生活垃圾分类的行动中，某社区为了了解居民掌握垃圾分类知识的情况进行调查．其中A，B两小区分别有500名居民参加了测试，社区从中各随机抽取50名居民成绩进行整理得到部分信息： 信息一 A小区50名居民成绩的频数直方图如图（每一组含前一个边界值，不含后一个边界值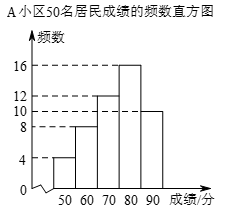）． 信息二 如图中，从左往右第四组的成绩如下： 信息三 A，B两小区各50名居民成绩的平均数、中位数、众数、优秀率（80分及以上为优秀）、方差 等数据如下（部分空缺）： 根据以上信息，回答下列问题： （1）求A小区50名居民成绩的中位数； （2）请估计A小区500名居民成绩能超过平均数的人数； （3）请尽量从多个角度，选择合适的统计量分析A，B两小区参加测试的居民，掌握垃圾分类知识的情况．

19.(本小题8分) 请在平面直角坐标系中描出以下三点：A(-2，1)，B(3，1)，C(2，3)．并回答如下问题： （1）在平面直角坐标系中画出△ABC； （2）在平面直角坐标系中画出△A'B'C'；使它与△ABC关于x轴对称，并写出点C'的坐标； （3）判断△ABC的形状，并说明理由．

20.(本小题11分) 已知二元一次方程x+y=5，通过列举将方程的解写成表格的形式： 如果将二元一次方程的解所包含的未知数x的值对应直角坐标系中一个点的横坐标，未知数y的值对应这个点的纵坐标，这样一个二元一次方程的解，就可以对应直角坐标系中的一个点，例如方程x+y=5的解的对应点是(2，3)． （1）表格中的m= ，n= ； （2）通过以上确定对应点坐标的方法，将表中给出的五个解依次转化为对应点的坐标，并在所给的直角坐标系中画出这五个点；根据这些点猜想方程x+y=5的解的对应点所组成的图形是，并写出它的两个特征：① ；② ； （3）若点P(-2a，a-1)恰好落在x+y=5的解对应的点组成的图形上，求a的值．

21.(本小题9分) 如图，在△ABC中，AD平分∠BAC，AE⊥BC于点E，且∠C＞∠B． （1）求证：∠DAE=(∠C-∠B)； （2）若把题干中的条件“AE⊥BC于点E”改为“点F为线段AD上一点且FE⊥BC于点E”，其他条件不变，请画出新图形，并证明∠DFE=(∠C-∠B)．

22.(本小题10分) 猕猴嬉戏是王屋山景区的一大特色，猕猴玩偶非常畅销．小李在某网店选中A，B两款猕猴玩偶，决定从该网店进货并销售．两款玩偶的进货价和销售价如下表： （1）第一次小李用1100元购进了A，B两款玩偶共30个，求两款玩偶各购进多少个． （2）第二次小李进货时，又购进两款玩偶共30个，规定购进B款玩偶a个（a≥20），应如何设计进货方案才能获得最大利润，最大利润是多少？ （3）小李第二次进货时采取了（2）中设计的方案，并且两次购进的玩偶全部售出，请从利润率的角度分析，对于小李来说哪一次更合算？（注：利润率

23.(本小题12分) 如图，在平面直角坐标系中，直线y=-2x+12与x轴交于点A，与y轴交于点B，与直线y=x交于点C． （1）求点C的坐标． （2）若P是x轴上的一个动点，直接写出当△POC是等腰三角形时点P的坐标． （3）在直线AB上是否存在点M，使得△MOC的面积是△AOC面积的2倍？若存在，请求出点M的坐标；若不存在，请说明理由．