九年级数学上学期期末综合练习(二)(北师版)
满分120分 答题时间100分钟
已经有0位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
17.(本小题9分)
为落实我市关于开展中小学课后服务工作的要求,某学校开设了四门校本课程供学生选择:A.趣味数学;B.博乐阅读;C.快乐英语;D.硬笔书法.某年级共有100名学生选择了A课程,为了解本年级选择A课程学生的学习情况,从这100名学生中随机抽取了30名学生进行测试,将他们的成绩(百分制)分成六组,绘制成频数分布直方图.
(1)已知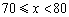 这组的数据为:72,73,74,75,76,76,79.则这组数据的中位数是 ;众数是 ;
这组的数据为:72,73,74,75,76,76,79.则这组数据的中位数是 ;众数是 ;
(2)根据题中信息,估计该年级选择A课程学生成绩在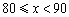 的总人数;
的总人数;
(3)该年级学生小乔随机选取了一门课程,则小乔选中课程D的概率是 ;
(4)该年级每名学生选两门不同的课程,小张和小王在选课程的过程中,若第一次都选了课程C,那么他俩第二次同时选择课程A或课程B的概率是多少?请用列表法或树状图的方法加以说明.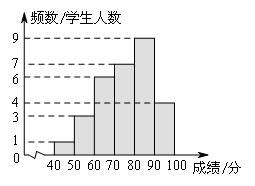
核心考点: 数据的分析 用树状图或表格求概率
-
23.(本小题11分)
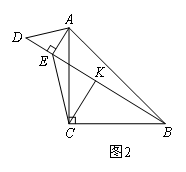
如图,在Rt△ABC中,∠ACB=90°,∠BAC=α,点D在边AC上(不与点A,C重合),连接BD,点K为线段BD的中点,过点D作DE⊥AB于点E,连接CK,EK,CE,将△ADE绕点A顺时针旋转一定的角度(旋转角小于90°).
(1)如图1,若α=45°,则△ECK的形状为 ;
(2)在(1)的条件下,若将图1中的△ADE绕点A旋转,使得D,E,B三点共线,点K为线段BD的中点,如图2所示,求证:BE-AE=2CK;
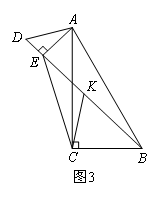
(3)若△ADE绕点A旋转至图3位置时,使得D,E,B三点共线,点K仍为线段BD的中点,请你直接写出BE,AE,CK三者之间的数量关系(用含α的三角函数表示).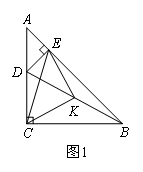
核心考点: 相似三角形的判定和性质 类比探究




















