九年级数学 解直角三角形单元练习(一)(冀教版)
满分120分 答题时间100分钟
已经有0位用户完成了练习
单选题(本大题共小题, 共分)
填空题(本大题共小题, 共分)
解答题(本大题共小题, 共分)
-
21.(本小题10分)
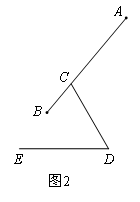
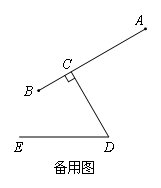
(2021鄂尔多斯)图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图,托板长AB=115mm,支撑板长CD=70mm,托板AB固定在支撑板顶点C处,且CB=35mm,托板AB可绕点C转动,支撑板CD可绕点D转动,∠CDE=60°.
(1)若∠DCB=70°时,求点A到直线DE的距离;(计算结果精确到个位)
(2)为了观看舒适,把(1)中∠DCB=70°调整为90°,再将CD绕点D逆时针旋转,使点B落在直线DE上即可,求CD旋转的角度.(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2,sin26.6°≈0.4,cos26.6°≈0.9,tan26.6°≈0.5,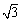 ≈1.7)
≈1.7)
核心考点: 锐角三角函数的应用
-
23.(本小题11分)
观察猜想
(1)如图1,在Rt△ABC中,∠ACB=90°,∠BAC=30°,点D与点C重合,点E在斜边AB上,连接DE,且DE=AE,将线段DE绕点D顺时针旋转90°得到线段DF,连接EF,则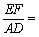 ,sin∠ADE= ;
,sin∠ADE= ;
探究证明
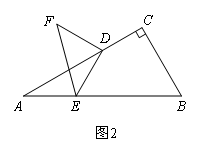
(2)在(1)中,如果将点D沿CA方向移动,使CD=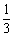 AC,其余条件不变,如图2,上述结论是否保持不变?若改变,请求出具体数值:若不变,请说明理由;
AC,其余条件不变,如图2,上述结论是否保持不变?若改变,请求出具体数值:若不变,请说明理由;
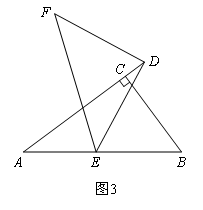
(3)如图3,在△ABC中,∠ACB=90°,∠CAB=α,点D在边AC的延长线上,E是AB上任意一点,连接DE.ED=nAE,将线段DE绕着点D顺时针旋转90°至点F,连接EF.求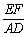 和sin∠ADE的值分别是多少?(请用含有n,α的式子表示)
和sin∠ADE的值分别是多少?(请用含有n,α的式子表示)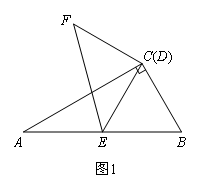
核心考点: 锐角三角函数 类比探究























