角的相关计算和证明(过程训练)(三)(通用版)
满分100分 答题时间30分钟
已经有1975位用户完成了练习
单选题(本大题共小题, 共分)
-
1.(本小题12分)
已知:如图,在△ABC中,AD是∠BAC的角平分线,∠B=∠1,∠ADC=80°.
求∠C的度数.
解:如图,
∵∠ADC是△ABD的一个外角(外角的定义)
∴∠ADC=∠1+∠B(三角形的一个外角等于和它不相邻的两个内角的和)
∵∠B=∠1(已知)
∴∠ADC=2∠1(等式的性质)
∵∠ADC=80°(已知)
∴
横线处应填写的过程,顺序正确的是( )
①∵AD是∠BAC的角平分线(已知)
②∵∠DAC=∠1=40°(已知)
③∵∠ADC=80°(已知)
④∴∠C=180°-∠DAC-∠ADC
=180°-40°-80°
=60°(三角形的内角和是180°)
⑤∴∠DAC=∠1=40°(角平分线的定义)
核心考点: 三角形外角定理 三角形的内角和是180°
-
2.(本小题12分)
已知:如图,在△ABC中,AD是∠BAC的角平分线,∠B=∠1,∠ADC=80°.
求∠C的度数.
解:如图,
∵∠ADC是△ABD的一个外角(外角的定义)
∴∠ADC=∠1+∠B(三角形的一个外角等于和它不相邻的两个内角的和)
∵∠B=∠1(已知)
∴∠ADC=2∠1(等式的性质)
∵∠ADC=80°(已知)
∴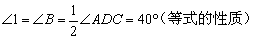
横线处应填写的过程,顺序正确的是( )
①∵∠ADC=80°(已知)
②∵AD是∠BAC的角平分线(已知)
③∴∠C=180°-∠B-∠BAC
=180°-40°-80°
=60°(三角形的内角和是180°)
④∴∠DAC=∠1=40°(角平分线的定义)
⑤∴∠BAC=2∠1=80°(角平分线的定义)
核心考点: 三角形外角定理 三角形的内角和是180°
-
3.(本小题12分)
如图,在△ABC中,∠ACB=90°,E是BC边上的一点,过C作CF⊥AE,垂足为F,
过B作BD⊥BC,交CF的延长线于点D.若∠1=25°,求∠D的度数.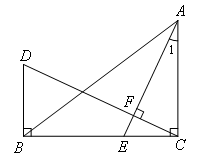
解:如图,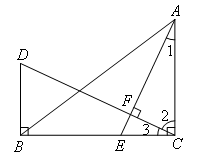
∵∠1=25°(已知)
∴∠3=25°(等量代换)
∵BD⊥BC(已知)
∴∠DBC=90°(垂直的性质)
∴∠D=90°-∠3
=90°-25°
=65°(直角三角形两锐角互余)
横线处应填写的过程,顺序正确的是( )
①∵∠ACB=90°(已知)
②∵CF⊥AE(已知)
③∴∠3=∠1(同角的余角相等)
④∴∠AFC=90°(垂直的性质)
⑤∴∠1+∠2=90°(直角三角形两锐角互余)
⑥∴∠2+∠3=90°(余角的定义)
核心考点: 直角三角形两锐角互余 同角(等角)的余角相等
-
4.(本小题12分)
如图,在△ABC中,∠ACB=90°,E是BC边上的一点,过C作CF⊥AE,垂足为F,过B作BD⊥BC,交CF的延长线于点D.若∠1=25°,求∠D的度数.
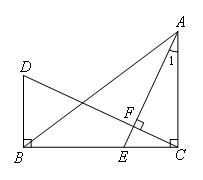
解:如图,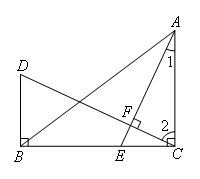
∵BD⊥BC(已知)
∴∠DBC=90°(垂直的性质)
∵CF⊥AE(已知)
∴∠AFC=90°(垂直的性质)
∵∠1=25°(已知)
∴∠2=90°-∠1
=90°-25°
=65°(直角三角形两锐角互余)
∴∠D=65°(等量代换)
横线处应填写的过程,顺序正确的是( )
①∵∠ACB=90°(已知)
②∵∠DBC+∠ACB=180°(同旁内角互补)
③∴∠DBC+∠ACB=180°(等式的性质)
④∴∠D=∠2(两直线平行,内错角相等)
⑤∴BD∥AC(同旁内角互补,两直线平行)
核心考点: 直角三角形两锐角互余 平行的性质和判定
-
5.(本小题13分)
已知:如图,在△ABC中,∠BAC=50°,∠ABC=60°,AD⊥BC,BE⊥AC,
垂足分别为D,E,AD,BE相交于点H,求∠AHB的度数.
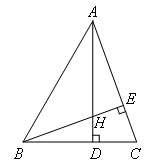
解:如图,
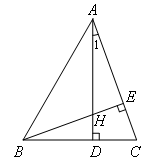
∵BE⊥AC(已知)
∴∠AEH=90°(垂直的性质)
∵∠AHB是△AHE的一个外角(外角的定义)
∴∠AHB=∠1+∠AEH
=20°+90°
=110°(三角形的一个外角等于和它不相邻的两个内角的和)
横线处应填写的过程,顺序正确的是( )
①∵∠BAC=50°,∠ABC=60°(已知)
②∵AD⊥BC(已知)
③∴∠ADC=90°(垂直的性质)
④∴∠C=180°-∠BAC-∠ABC
=180°-50°-60°
=70°(三角形的内角和是180°)
⑤∴∠1=90°-∠C
=90°-70°
=20°(直角三角形两锐角互余)
核心考点: 三角形外角定理 三角形的内角和是180° 垂直的性质
-
6.(本小题13分)
已知:如图,在△ABC中,∠BAC=50°,∠ABC=60°,AD⊥BC,BE⊥AC,垂足分别为D,E,AD,BE相交于点H,求∠AHB的度数.
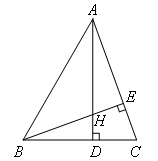
解:如图,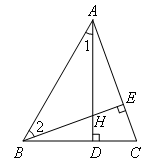
∵AD⊥BC(已知)
∴∠ADB=90°(垂直的性质)
∵∠ABC=60°(已知)
∴∠1=90°-∠ABC
=90°-60°
=30°(直角三角形两锐角互余)
∴∠AHB=180°-∠1-∠2
=180°-30°-40°
=110°(三角形的内角和是180°)
横线处应填写的过程,顺序正确的是( )
①∵BE⊥AC(已知)
②∵AD⊥BC(已知)
③∵∠BAC=50°(已知)
④∴∠2=90°-∠BAC
=90°-50°
=40°(直角三角形两锐角互余)
⑤∴∠BEA=90°(垂直的性质)
⑥∴∠ADB=90°(垂直的性质)
核心考点: 三角形的内角和是180° 垂直的性质
-
7.(本小题13分)
如图,已知∠A=∠ABC,∠CBD=∠D,BD平分∠ABC,点E在BC的延长线上.
求证:CD是∠ACE的角平分线.
证明:如图,
设∠CBD=α,则∠D =∠CBD=α.
∵∠DCE是△CBD的一个外角(外角的定义)
∴∠DCE=∠D+∠CBD=2α(三角形的一个外角等于和它不相邻的两个内角的和)
∵BD平分∠ABC(已知)
∴∠ABC=2∠CBD=2α(角平分线的定义)
∴CD是∠ACE的角平分线(角平分线的定义)
横线处应填写的过程,顺序正确的是( )
①∵∠A=∠ABC(已知)
②∵∠ACE是△ABC的一个外角(外角的定义)
③∵CD是∠ACE的角平分线(已知)
④∴∠ACE=2∠DCE(等式的性质)
⑤∴∠ACE=∠A+∠ABC
=2α+2α
=4α(三角形的一个外角等于和它不相邻的两个内角的和)
⑥∴∠A=2α(等量代换)
核心考点: 角平分线的性质 三角形外角定理












