综合复习之应用题（二）（通用版）-九年级试卷-众享学科测评

综合复习之应用题（二）（通用版）

满分100分答题时间30分钟

已经有1126位用户完成了练习

单选题(本大题共小题，共分)

1.(本小题12分) 为改善城市生态环境，实现城市生活垃圾减量化、资源化、无害化的目标，某市决定从3月1日起，在全市部分社区试点实施生活垃圾分类处理．某街道计划建造垃圾初级处理点20个，解决垃圾投放问题．A，B两种类型处理点的占地面积、可供使用的居民楼幢数及造价见下表： 已知可供建造垃圾初级处理点的占地面积不超过，该街道共有490幢居民楼． 设建造A类型处理点x个． （1）欲求满足条件的建造方案共有几种，根据题意，所列方程（组）或不等式（组）正确的是( )

2.(本小题12分) （上接第1题）（2）设建造垃圾初级处理点的总费用为w万元，则w与x之间的函数关系式为( )；当x=( )时，总费用最少．

3.(本小题12分) 为了保护环境，某化工厂一期工程完成后购买了4台甲型和3台乙型污水处理设备，共花费资金75万元，已知每台乙型设备的价格是每台甲型设备价格的75%．实际运行中发现，每台甲型设备每月能处理污水200吨，每台乙型设备每月能处理污水160吨，且每年用于每台甲型设备的各种维护费和电费为1万元，每年用于每台乙型设备的各种维护费和电费为1.5万元．今年该厂二期工程即将完成，产生的污水将大大增加，于是该厂决定再购买甲、乙两种设备共8台用于二期工程的污水处理，预算本次购买资金不超过84万元，预计二期工程完成后每月将产生不少于1300吨污水． （1）每台甲型设备和每台乙型设备的价格分别为( )元．

4.(本小题12分) （上接第3题）（2）请求出用于二期工程的污水处理设备的所有购买方案.设二期工程中，购买甲型设备x台，根据题意，下列不等式（组）正确的是( )

5.(本小题13分) （上接第3，4题）（3）若两种设备的使用年限均为10年，设用于二期工程的污水处理设备的总费用为w元，则w与x之间的函数关系式为，当x= 时，总费用最少( ) （总费用=设备购买费+各种维护费和电费）

6.(本小题13分) 为推进节能减排，发展低碳经济，我市某“用电大户”用480万元购得“变频调速技术”后，进一步投入资金1520万元购买配套设备，以提高用电效率，达到节约用电的目的．已知该“用电大户”生产的产品每件成本费为40元．经过市场调研发现：该产品的销售单价，需定在100元到300元之间较为合理．当销售单价定为100元时，年销售量为20万件；当销售单价超过100元，但不超过200元时，每件产品的销售价格每增加10元，年销售量将减少0.8万件；当销售单价超过200元，但不超过300元时，每件产品的销售价格每增加10元，年销售量将减少a万件．设销售单价为x（元），年销售量为y（万件），年获利为w（万元）． （1）若求出当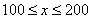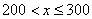，时，y与x之间的函数关系式分别是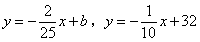，则a，b的值分别为( )

7.(本小题13分) （上接第6题）（2）在（1）的条件下，当，时，第一年的年获利w与x之间的函数关系式分别是( )（年获利=年销售额-生产成本-其他成本）

8.(本小题13分) （上接第6，7题）（3）若该“用电大户”在第二年把该产品的销售单价定在超过100元，但不超过200元的范围内，并希望到第二年年底，除去第一年的最大盈利（或最小亏损）后，两年的总盈利为1842万元，根据题意可列方程( )