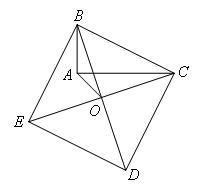
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCDE,设正方形的中心为O,连接AO,如果AB=4,AO=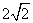 ,那么AC的长为( )
,那么AC的长为( )
- A.
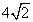
- B.
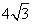
- C.
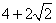
- D.8
答案
正确答案:D
知识点:略
如图,过点O作OF⊥OA交AC于点F,
则∠AOF=90°.
由正方形的性质可得,∠BOC=90°,∠OBC=∠OCB=45°,OB=OC,
∴∠AOF-∠BOF=∠BOC-∠BOF,
即∠1=∠2.
在Rt△ABC中,∠BAC=90°,
∴∠ABC+∠ACB=90°,
即∠3+∠OBC+∠ACB=90°,
在Rt△OBC中,∠BOC=90°,
∴∠OBC+∠OCB=90°,
即∠OBC+∠4+∠ACB=90°,
∴∠3=∠4,
∴△AOB≌△FOC(ASA),
∴OF=OA=![]() ,FC=AB=4.
,FC=AB=4.
在Rt△AOF中,∠AOF=90°,OF=OA=![]() ,
,
由勾股定理得,AF=4,
∴AC=AF+FC=8.
略








