如图所示，△ABC中，AB=3，AC=7，AD为△ABC的中线，求AD的取值范围．

先在图上走通思路后再填写空格内容：
1．因为AD为△ABC的中线，考虑                                （辅助线叙述）；
2．进而利用全等三角形的判定         ，证明       ≌       ；
3．由全等可得                ；
4．观察图形，2AD放在△       中，利用三角形的三边关系，可得2以上空缺处依次所填最恰当的是(    )

• A.①延长AD到F，使DF=AD；
  ②SAS，△BDF，△CDA；
  ③∠DBF=∠C
  ④ABF
• B.①延长AD到F，使DF=AD，连接BF；
  ②SAS，△BDF，△CDA；
  ③FB=AC
  ④ABF
• C.①延长AD到F，使DF=AD，过点B作BF∥AC；
  ②SAS，△BDF，△CDA；
  ③FB=AC
  ④ABF
• D.①延长AD到F，使DF=AD，连接BF；
  ②SSA，△BDF，△CDA；
  ③FB=AC
  ④ABF

答案

正确答案：B

知识点：略  

如图，先在图上走通思路，

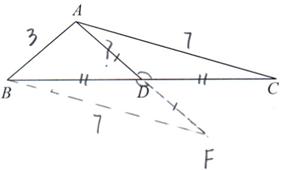
AD为△ABC的中线，见中线，要倍长，
延长AD到F，使DF=AD，连接BF；
倍长之后证全等，因为AD为△ABC的中线，所以BD=CD，
又因为DF=DA，∠BDF=∠CDA，
利用SAS可以证得△BDF≌△CDA；
然后根据全等三角形对应边相等来转移边，可得BF=CA=7；
由于AF=2AD，因此可以把2AD放在△ABF中，
利用三角形的三边关系，可得BF-AB结合已知条件可知7-3<2AD<7+3，所以2故选B．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>