已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,
求证:∠C=∠BAE.

证明:如图, .

∵AE是△ABD的中线
∴BE=ED
在△ABE和△FDE中

∴△ABE≌△FDE(SAS)
∴
∵CD=AB
∴CD=FD
∵∠ADF=∠ADB+∠1
∴∠ADF=∠ADB+∠B
∵∠ADC为△ABD的一个外角
∴∠ADC=∠B+∠BAD
∵∠ADB=∠BAD
∴∠ADF=∠ADC
在△FAD和△CAD中

∴△FAD≌△CAD(SAS)
∴
∴∠C=∠BAE
请你仔细观察下列序号所代表的内容,然后判断:
①延长AE到F,连接DF,使得DF∥AB;
②延长AE到F,使得EF=AE,连接DF;
③延长AE到F,使得EF=AE,连接DF,过D作DF∥AB;
④AB=FD,AE=EF;
⑤AB=FD,∠BAE=∠F,∠B=∠1;
⑥AB=FD;
⑦AF=AC;
⑧∠F=∠C.
以上空缺处依次所填最恰当的是( )
- A.①⑤⑧
- B.③④⑧
- C.③⑥⑦
- D.②⑤⑧
答案
正确答案:D
知识点:略
如图,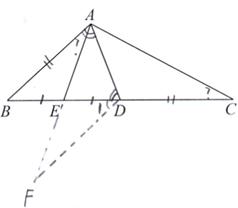
AE为△ABD的中线,见中线,要倍长,
延长AE到F,使得EF=AE,连接DF;
倍长之后证全等,利用SAS可以证得△ABE≌△FDE;
根据全等,可以转移边、转移角,结合后面的步骤,可知用到了等量代换,此处应该由全等得到AB=FD,∠BAE=∠F,
∠B=∠1;然后通过转移角,证得∠ADF=∠ADC,进而由SAS证明△FAD≌△CAD,由全等可得∠F=∠C,结合前面由第一次全等证得的∠BAE=∠F,等量代换得到∠C=∠BAE.
故选D.
略











