在四边形ABCD中，BA=BC，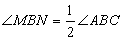
．
（1）如图，当点M，N分别在AD，CD上时，若∠BAD=∠BCD=90°，求证：MN=AM+CN．
解题思路：（1）如图，延长NC到E，使CE=AM，连接BE．
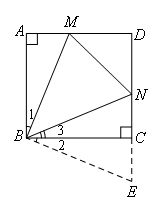
由∠BAD=∠BCD=90°，得∠BAM=∠BCE，因为BA=BC，AM=CE，因此根据三角形全等的判定定理 ，可以得到△BAM≌△BCE，由全等的性质得到 ；
又因为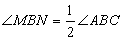，可得 ，因此根据三角形全等的判定定理SAS，可以得到 ，由全等的性质得到MN=EN；
通过等量代换可得MN=EN=CE+CN=AM+CN．
①ASA；②SAS；③SSA；④AM=CE，BM=BE；⑤∠1=∠2，BM=BE；⑥∠1=∠2；⑦∠MBN=∠EBN；⑧△BMN≌△BEN；⑨△BAM≌△BCE．
以上横线处，依次所填正确的是( )
．
- A.③⑤⑦⑨
- B.①④⑥⑧
- C.②⑤⑥⑨
- D.②⑤⑦⑧
答案
正确答案：D
知识点：略
要证MN=AM+CN，这是几条线段间的数量关系，
考虑利用截长补短转化成两条线段间的等量关系，在这里使用补短法．
如图，延长NC到E，使CE=AM，连接BE．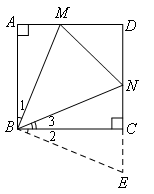
∵∠BAD=∠BCD=90°
∴∠BAM=∠BCE
∵BA=BC，AM=CE
∴△BAM≌△BCE（SAS）
∴∠1=∠2，BM=BE
∵∠MBN=
∠ABC
∴∠1+∠3=∠MBN
∴∠2+∠3=∠MBN
即∠MBN=∠EBN
∵BM=BE，BN=BN
∴△MBN≌△EBN（SAS）
∴MN=EN
=CE+CN
=AM+CN
因此横线处依次所填正确的是②⑤⑦⑧．
故选D．
略
WORD格式（