(上接第4题)(2)如图,当点M,N分别在AD,CD上时,若∠A=∠D,AD∥BC,为证明MN=AM+CN,需要作出辅助线,下列辅助线的叙述和证明思路正确的是( )
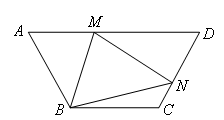
- A.延长NC到E,使AM=CE;先证明△BAM≌△BCE,再证明△BMN≌△BEN,通过等量代换得MN=AM+CN
- B.延长NC到E,使CE=AM,连接BE;先证明△BAM≌△BCE,再证明△BMN≌△BEN,通过等量代换得MN=AM+CN
- C.延长AB到E,使BE=BA,连接CE;先证明△BAM≌△BCE,再证明△BMN≌△BEN,通过等量代换得MN=AM+CN
- D.延长AB到E,使BE=BA,连接CE;先证明△BMN≌△BEN,再证明△BAM≌△BCE,通过等量代换得MN=AM+CN
答案
正确答案:B
知识点:略
类比(1)中的思路和字母把三角形全等照搬到(2)中,
先得到△BAM≌△BCE(SAS),
根据全等的性质,得到对应边、对应角的关系∠1=∠2,BM=BE,
转角得到∠MBN=∠EBN,可证△BMN≌△BEN(SAS),
进而推导出MN,AM,CN这三条线段之间的数量关系为MN=AM+CN.
如图,延长NC到E,使CE=AM,连接BE.
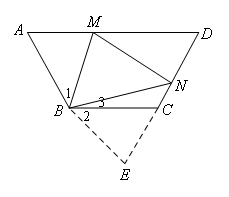
∵BC∥AD
∴∠D=∠BCE
∵∠A=∠D
∴∠A=∠BCE
∵AB=CB,AM=CE
∴△BAM≌△BCE(SAS)
∴∠1=∠2,BM=BE
∵∠MBN=![]() ∠ABC
∠ABC
∴∠1+∠3=∠MBN
∴∠2+∠3=∠MBN
即∠MBN=∠EBN
∵BM=BE,BN=BN
∴△MBN≌△EBN(SAS)
∴MN=EN
=CE+CN
=AM+CN
故选B.
略








