已知:如图,点C,D在线段BE上,且BD=EC,CA⊥AB于A,DF⊥EF于F,且AB=EF.
求证:△ABD≌△FEC.
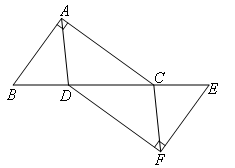
证明:如图,
∵CA⊥AB,DF⊥EF
∴∠BAC=∠EFD=90°
∵BD=CE
∴BD+DC=CE+DC
即BC=ED
∴∠B=∠E
在△ABD和△FEC中
∴
请你仔细观察下列序号所代表的内容:
① ;②
;② ;
;
③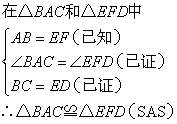 ;④
;④ ;⑤
;⑤ ;
;
⑥△ABD≌△FCE(SSA);⑦△ABD≌△FEC(SAS).
以上空缺处依次所填最恰当的是( )
- A.①④⑦
- B.②④⑦
- C.③⑤⑥
- D.①⑤⑧
答案
正确答案:A
知识点:略
要证△ABD≌△FEC,需要找三组条件,
已知AB=EF,BD=EC,还需找一组条件;
由题可知∠BAC=∠EFD=90°,由BD=EC可得BC=ED,
加上AB=EF,由HL可以证得△BAC≌△EFD,
由全等三角形对应角相等可得∠B=∠E;
进而由SAS可以证得△ABD≌△FEC.
空缺处依次所填最恰当的是①④⑦.
故选A.
略








 ;②
;② ;
;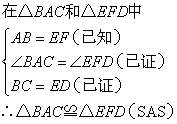 ;④
;④ ;⑤
;⑤ ;
;