如图,在菱形ABCD中,AB=2,∠B=60°,E,F分别是边BC,CD中点,则△AEF的周长为( )

- A.
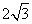
- B.
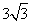
- C.
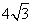
- D.3
答案
正确答案:B
知识点:略
如图,连接AC,BD,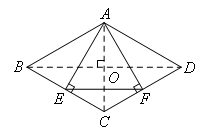
∵四边形ABCD是菱形,
∴AB=BC,
又∵∠ABC=60°,
∴△ABC是等边三角形,∠ABO=30°,
∴AB=AC=2,
∵点E是边BC的中点,
∴EB=EC=1,∠EAC=30°,
在Rt△AEC中,∠AEC=90°,AC=2,EC=1,
由勾股定理得,AE=![]() ,
,
同理可得AF=![]() .
.
在Rt△ABO中,∠AOB=90°,∠ABO=30°,AB=2,
∴AO=1,OB=![]() ,
,
∴BD=![]() ,
,
∵E,F分别是边BC,CD中点,
∴EF是△BCD的中位线,
∴![]() ,
,
∴C△AEF=AE+AF+EF=![]() .
.
略








