如图所示,∠ACB=3∠B,∠1=∠2,CD⊥AD于点D,若AC=5,CD=3,则AB的长为( )
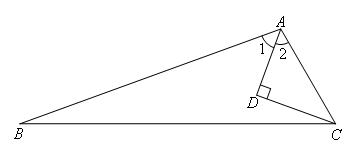
- A.10
- B.11
- C.12
- D.15
答案
正确答案:B
知识点:略
分析:由题中条件∠1=∠2,CD⊥AD,是“三线”中“两线”重合,可考虑通过等角的余角相等或全等证等腰,进而解决问题.
如图,延长CD交AB于点E,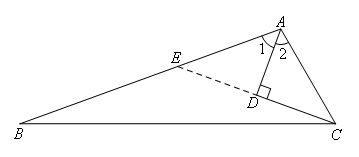
∵AD⊥CD,
∴∠ADC=∠ADE=90°
∴∠1+∠AEC=90°,∠2+∠ACE=90°,
∵∠1=∠2,
∴∠AEC=∠ACE
∴AC=AE
∴CE=2CD,
又∵∠AEC=∠B+∠ECB,∠ACB=3∠B,
∴3∠B=∠ECB+∠B+∠ECB,
∴∠B=∠ECB
∴BE=CE,
∴BE=2CD,
∴AB=AE+BE=AC+2CD,
∵AC=5,CD=3,
∴AB=11,
故选B.
略








