如图,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若DE=1,则BC的长为( )

- A.
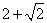
- B.
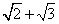
- C.
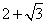
- D.3
答案
正确答案:A
知识点:略
分析:因为AD平分∠BAC,DE⊥AB,考虑过点D作DF⊥AC于点F,根据角平分线的性质得DE=DF=1,且同时把∠B=30°,∠C=45°都放到了直角三角形中.
解:如图,过点D作DF⊥AC于点F,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,DE=1,
.DE=DF=1,∠BED=∠DFC=90°.
在Rt△BED中,∠BED=90°,∠B=30°,
∴BD=2DE=2.
∵∠DFC=90°,∠C=45°,
∴∠FDC=∠C=45°.
∴CD=DF=1.
在Rt△CDF中,由勾股定理,得
CD=![]() .
.
∴BC=BD+CD=![]() .
.
故选A
略








