如图，在△ABC中，点Q，P分别是边AC，BC上的点，AQ=PQ，PR⊥AB于R，PS⊥AC于S，且PR=PS，下面四个结论：①AP平分∠BAC；②AS=AR；③BP=QP；④QP∥AB．其中一定正确的是(    )

如图：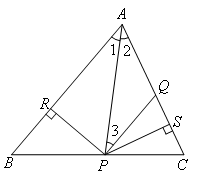

∵PR⊥AB，PS⊥AC，且PR=PS，
∴点P在∠BAC的平分线上，
即：AP平分∠BAC，①正确；
由结论①可知∠1=∠2，
又∵∠PRA=∠PSA=90°，
∴∠APR=∠APS，
即：PA平分∠RPS，
∴AS=AR，②正确；
由结论①可知∠1=∠2，
∵AQ=PQ，
∴∠2=∠3，
∴∠1=∠3，
∴QP∥AB，④正确；
BP和QP无法证明相等，故③不一定正确．
故选B．

略