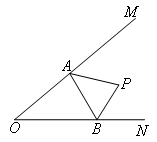
如图所示，∠MON=40°，P为∠MON内一个定点，A为OM上一动点，B为ON上一动点，则当△PAB的周长取最小值时，∠APB的度数为(    )

特征：
定点：P；
动点：A，B；
动点A在OM上运动，动点B在ON上运动，
所求为△PAB的周长最小，属于轴对称路径最短问题．
操作：
应作定点关于定直线的对称点．
如图所示，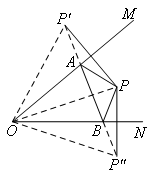

分别作点P关于OM，ON的对称点，，
连接，，．分别交OM，ON于点A，B，
连接PA，PB，此时△PAB的周长最小，
最小值即为的长．
由对称可得，，，
，
∴，
∴．
∴，，
∴∠APB=∠APO+∠BPO=100°．
故选B．

略