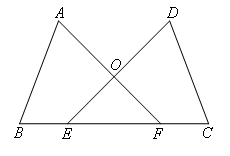
已知:如图,点B,E,F,C在同一直线上,AB=DC,BE=CF,∠B=∠C.
求证:OA=OD.
证明:如图,过点O作OG⊥EF于G.
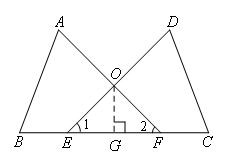
∵BE=CF
∴BE+EF=CF+EF
即BF=CE
在△ABF和△DCE中
∴△ABF≌△DCE( )
∴∠2=∠1(全等三角形对应角相等)
AF=DE(全等三角形对应边相等)
∵OG⊥EF
∴∠OGE=∠OGF=90°
在△OEG和△OFG中
∴△OEG≌△OFG( )
∴OE=OF(全等三角形对应边相等)
∴AF-OF=DE-OE
即OA=OD
请你仔细观察下列序号所代表的内容:
①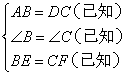 ;②
;②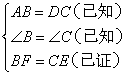 ;③SAS;④SSA;⑤ASA;
;③SAS;④SSA;⑤ASA;
⑥AAS;⑦ ;⑧
;⑧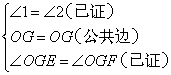 .
.
以上空缺处依次所填正确的是( )
- A.②③⑦⑥
- B.①④⑦⑥
- C.②③⑧⑤
- D.①④⑧⑤
答案
正确答案:A
知识点:全等三角形的性质 全等三角形的判定 全等三角形之辅助线
观察图形,题中已知AB=DC,BE=CF,∠B=∠C,
由BE=CF可得BF=CE,
可以证得△ABF≌△DCE(SAS),
得到∠2=∠1,AF=DE;
结合要证明的结论,由OG⊥EF可以得到∠OGE=∠OGF=90°,
OG是公共边,可以证得△OEG≌△OFG(AAS),
得到OE=OF,
所以AF-OF=DE-OE,即OA=OD.
故选A.
略









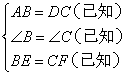 ;②
;②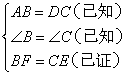 ;③SAS;④SSA;⑤ASA;
;③SAS;④SSA;⑤ASA; ;⑧
;⑧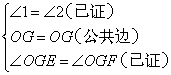 .
.