先阅读，再解答问题：
恒等变形，是代数式求值的一个很重要的方法．利用恒等变形，可以把无理数运算转化为有理数运算，可以把次数较高的代数式转化为次数较低的代数式．
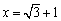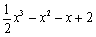例如：当时，求的值．
为解答这道题，若直接把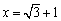代入所求的式中，进行计算，显然很麻烦，我们可以通过恒等变形，对本题进行解答．
方法：将条件变形，因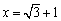，得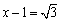，再把等式两边同时平方，把无理数运算转化为有理数运算．
由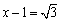，可得x²-2x-2=0，即x²-2x=2，x²=2x+2．
原式．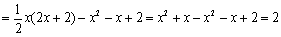
请参照以上的解决问题的思路和方法，解决以下问题：
（1）若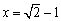，求2x³+4x²-3x+1的值；
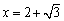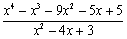（2）已知，求的值．

答案

（1）；
（2）．

知识点：二次根式的计算  

解：（1）∵x=-1，
∴x+1=，
∴(x+1)²=2，
即x²+2x+1=2，
∴x²+2x=1，
∴原式=2x(x²+2x)-3x+1
=2x-3x+1
=-x+1
=-(-1)+1
=2-；
（2）∵x=2+，
∴x-2=，
∴(x-2)²=3，
即x²-4x+4=3，
∴x²-4x=-1或x²=4x-1，
∴原式=
=(16x²-8x+1-4x²+x-36x+9-5x+5)
=[12(4x-1)-48x+15)
=(48x-12-48x+15)
=×3
=．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>