如图1，我们在“格点”直角坐标系上可以清楚看到：要找AB或DE的长度，显然是转化为求Rt△ABC或Rt△DEF的斜边长．下面以求DE为例来说明如何解决：
从坐标系中发现：D(-7，5)，E(4，-3)．所以DF=|5-(-3)|=8，EF=|4-(-7)|=11，
所以由勾股定理可得：DE==．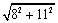
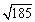下面请你参与：
（1）在图1中：AC=          ，BC=          ，AB=          ．
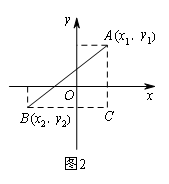
（2）在图2中：设A(x₁，y₁)，B(x₂，y₂)，试用x₁，x₂，y₁，y₂表示AC=       ，BC=        ，AB=        ．
（3）（2）中得出的结论被称为“平面直角坐标系中两点间距离公式”，请用此公式解决如下题目：
已知：A(2，1)，B(4，3)，C为坐标轴上的点，且使得△ABC是以AB为底边的等腰三角形．请求出点C的坐标．

答案

（1）4，3，5；
（2），，；
（3）(5，0)或(0，5)．

知识点：两点间的距离公式  勾股定理  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>