如图，抛物线y=-x²-2x+3的图象与x轴交于A，B两点（点A在点B的左边），与y轴交于点C．
（1）求A，B，C的坐标；
（2）过抛物线上一点F作y轴的平行线，与直线AC交于点G．若FG=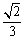AC，求点F的坐标；
（3）E(0，-2)，连接BE．将△OBE绕平面内的某点逆时针旋转90°得到△O′B′E′，O，B，E的对应点分别为O′，B′，E′．若点B′，E′两点恰好落在抛物线上，求点B′的坐标．

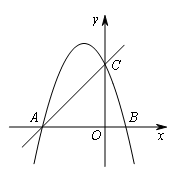
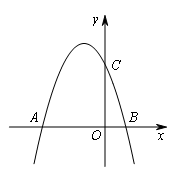
答案

（1）A(-3，0)；B(1，0)；C(0，3)；
（2）点F的坐标为(-1，4)，(-2，3)，(，)或(，)；
（3）点B′的坐标为(，)．

知识点：二次函数  存在性问题  旋转  

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>