如图,⊙O的两条弦AB,CD互相垂直,垂足为E,且AB=CD,已知CE=2,ED=8,则⊙O的半径是( )
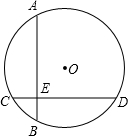
- A.3
- B.4
- C.5
- D.
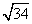
答案
正确答案:D
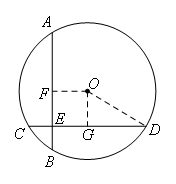 过O作OF⊥AB,OG⊥CD,连接OD,
过O作OF⊥AB,OG⊥CD,连接OD,
由垂径定理得到F为AB的中点,G为CD的中点,CE=2,ED=8,
∴AF=BF=CG=DG=5,
∵∠OFE=∠FEG=∠OGE=90°,
∴四边形OGEF为矩形,
又∵AB=CD,∴OF=OG,
∴四边形OGEF为正方形,
∴OG=EG=5-2=3,
在Rt△ODG中,根据勾股定理得:OD=![]() .
.
略








