如图,在三角形纸片ABC中,已知∠ABC=90°,AC=5,BC=4.过点A作直线l平行于BC,折叠三角形纸片ABC,使直角顶点B落在直线l上的点P处,折痕为MN.当点P在直线l上移动时,折痕的端点M,N也随之移动,若限定端点M,N分别在AB,BC边上(包括端点)移动,则线段AP长度的最大值与最小值之差为( )

- A.
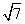
- B.
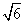
- C.
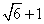
- D.
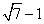
答案
正确答案:D
①我们首先求线段AP长度的最大最.
当A,M,P三点不共线时,在△AMP中,AP<AM+MP=AM+MB=3;
当A,M,P三点共线时,AP=AM+MP=3.
∴AP的最大值为3,此种情况如下图所示:
②再考虑求线段AP长度的最小值.
如图,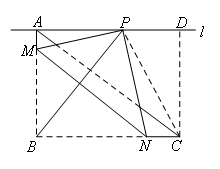
我们先将△ABC补成矩形ABCD,利用同样的方法来做,只需要求线段DP长度的最大值即可.
连接CP,若PD的长度最大,则CP的长度最大.
当P,N,C三点不共线时,在△CNP中,CP<CN+PN=CN+BN=4;
当P,N,C三点共线时,CP=4.
∴CP的最大值是4,
∴PD的最大值为![]() ,
,
∴AP的最小值为![]() ,此时情况如下图所示:
,此时情况如下图所示: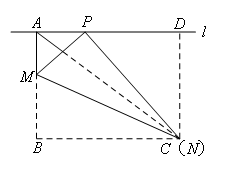
③∴AP的最大值与最小值之差是![]() ,故选D.
,故选D.
略








