如图,在等腰梯形ABCD中,AD∥BC,AD=6cm,BC=14cm,∠B=60°.P为下底BC上一点(不与点B,C重合),连接AP,过点P作射线PE交线段DC于点E,使得∠APE=∠B.若DE:EC=5:3,则BP=( )
- A.4cm或6cm
- B.3cm或8cm
- C.
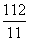 cm或
cm或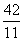 cm
cm - D.2cm或12cm
答案
正确答案:D
知识点:等腰梯形的性质 相似三角形的判定与性质
如图,过A作AF⊥BC于F,
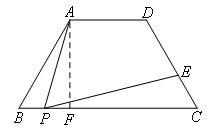
可求得BF=4cm,AB=8cm,CE=3cm.
由∠APC为△ABP的外角得∠APC=∠B+∠BAP,
∵∠B=∠APE,
∴∠CPE=∠BAP.
∵∠B=∠C,
∴△ABP∽△PCE,
∴![]() .
.
设BP=xcm,则PC=(14-x)cm,可得
![]() ,
,
解得x1=2,x2=12,
经检验都符合题意,即BP=2cm或BP=12cm.
略








