如图1,在正方形ABCD中,点M,N分别在AD,CD上,若∠MBN=45°,易证MN=AM+CN.
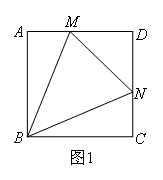
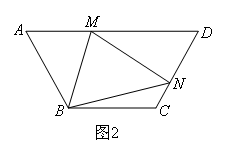
(1)如图2,在梯形ABCD中,BC∥AD,AB=BC=CD,点M,N分别在AD,CD上,若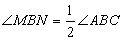,则
线段MN,AM,CN之间的数量关系为(    )

• A.
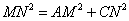
• B.
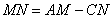
• C.
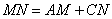
• D.

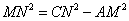
答案

正确答案：C

知识点：三角形全等性质与判定  中考数学几何中的类比探究  

如图，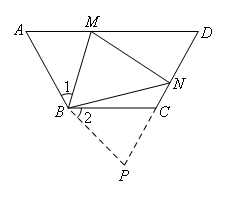

延长DC到P，使得CP=MA，连接PB．
易证得△AMB≌△CPB，
∴∠1=∠2，MB=PB，
∴∠ABC=∠MBP．
∵，
∴∠MBN=∠PBN，
又∵MB=PB，BN=BN，
∴△MBN≌△PBN，
∴MN=PN=CP+CN=AM+CN．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>