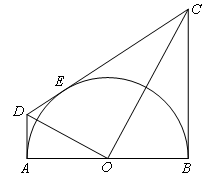
如图,AB为半圆O的直径,AD,BC分别与⊙O相切于点A,B,CD与⊙O相切于点E,AD与CD相交于点D,BC与CD相交于点C,连接OD,OC,下列结论:①AD+BC=CD;②∠DOC=90°;③;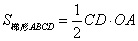
④OD²=DE•CD.其中正确的是(    )

如图所示，连接OE，则OE⊥CD．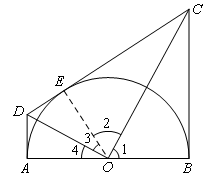

∵AD，BC为⊙O切线，
∴OA⊥AD，OB⊥BC，
容易证明△DAO≌△DEO，△CEO≌△CBO，
∴AD=DE,∠3=∠4；BC=EC，∠1=∠2．
∴AD+BC=DE+EC=CD，即结论①正确；
∵∠1+∠2+∠3+∠4=180°，∠3=∠4，∠1=∠2，
∴∠2+∠3=90°，
∴∠DOC=90°，即结论②正确；
，即结论③错误；
在Rt△DOC中，∵OE⊥CD，
容易证明△ODE∽△CDO，
∴，即OD²=DE•CD，即结论④正确．

略