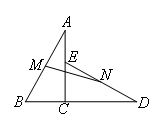
如图,将Rt△ABC(其中∠ACB=90°)绕点C顺时针旋转90°得到△DEC,M,N分别为AB,DE的中点,若MN=4,则AB的长为( )
- A.
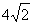
- B.4
- C.
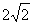
- D.8
答案
正确答案:A
知识点:直角三角形斜边中线等于斜边一半
1.思路分析
本题主要考查直角三角形斜边中线等于斜边一半及等腰直角三角形三边比例关系.解决此类问题需要注意:
①读题标注,明确目标.本题要求AB的长,条件只有MN=4,需要将MN的长度转移到AB上.
②梳理条件,合理转化.考虑到M,N是AB,DE的中点,结合直角三角形特征,可借助直角三角形斜边中线等于斜边一半的结论,求AB,只需求MC或NC,且MC=NC.
③回归目标,验证结果.结合△ABC旋转得到△DEC,由全等可知△MCN是等腰直角三角形,由MN=4及等腰直角三角形三边长比例关系,可求出MC长度,进而求得AB长.
2.解题过程
连接MC,NC
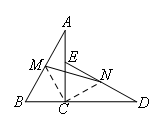

3.易错点
未考虑到旋转△ABC所得到的两个全等三角形,没有证出△MCN是等腰直角三角形.
等腰直角三角形三边长的比例关系记忆不准确,计算出错.
4.推荐视频
如果此题有问题,建议观看视频:“2013~2014八年级上册数学拔高训练北师版,初中数学勾股定理拔高课,第1讲直角三角形性质应用,03直角三角形斜边中线”
视频连接:http://v.xxt.cn/course/courseview.do?courseId=1598
略








