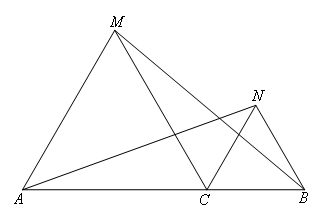
如图,C为线段AB上一点,在AB的同侧作等边△ACM和等边△BCN,连接AN,BM,
若∠MBN=20°,则∠ANB的大小是(    )

1.思路点拨
①分析图形，∠ANB=∠BNC+∠ANC=60°+∠ANC，只需求∠ANC；
②结合题目已知∠MBN=20°，且图形中相等的边比较多，故可借助全等转移角度，
又△ACN≌△MCB（SAS），可得∠ANC=∠MBC=60°-20°=40°，得到∠ANB=100°．
2.解题过程
如图，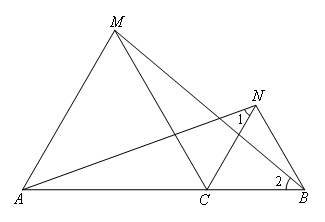

∵∠ACM=∠BCN=60°
∴∠ACM+∠MCN=∠BCN+∠MCN，即∠ACN=∠MCB
在△ACN和△MCB中，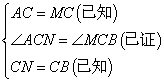

∴△ACN≌△MCB（SAS）
∴∠1=∠2，
∵∠MBN=20°，∠CBN=60°
∴∠1=∠2=40°
∴∠ANB=∠BNC+∠1=60°+40°=100°，
故选C
3.易错点
①常见的三角形全等结构不熟悉；
②不清楚相等的边比较多的时候，可以通过证明全等转移、整合条件．

略