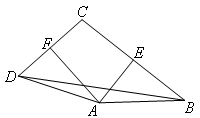
如图,在四边形ABCD中,AE⊥BC，且BE=CE,AF⊥CD,且CF=DF，若EAF=80°,∠CBD=30°,
则∠ABC的度数为(    )

如图，

连接AC
∵AE⊥BC，且BE=CE,AF⊥CD,且CF=DF，
∴△ABE≌△ACE,△ACF≌△ADF
∴AB=AC, AC=AD
∴AB=AC=AD
∵AF⊥DC，AE⊥BC
∴∠CAF=∠DAF，∠CAE=∠BAE
∴∠DAB=2∠EAF=160°
∵AB=AD
∴∠ABD=(180°-160°)÷2=10°
∴∠ABC=∠CBD+∠ABD =30°+10°=40°
故选B

略