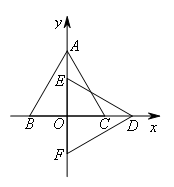
如图,在平面直角坐标系中,△ABC和△DEF为等边三角形,AB=DE,点B,C,D在x轴上,点A,E,F在y轴上,下面判断正确的是(    )

• A.△DEF是△ABC绕点O顺时针旋转90°得到的
• B.△DEF是△ABC绕点O逆时针旋转90°得到的
• C.△DEF是△ABC绕点O顺时针旋转60°得到的
• D.△DEF是△ABC绕点O顺时针旋转120°得到的

答案

正确答案：A

知识点：旋转的性质  坐标与图形变化—旋转  

要判断一个三角形是怎么样由另外一个三角形旋转得到的，需要找到“旋转中心，旋转方向，旋转角度”．
易知点O为旋转中心，点C和点F为一对对应点，
∵对应点与旋转中心所连线段的夹角等于旋转角，
∴∠FOC为旋转角，等于90°，
而旋转方向显然为顺时针，
∴△DEF是△ABC绕点O顺时针旋转90°得到的．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>