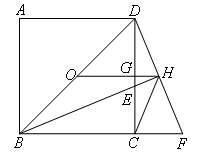
如图,O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交
BE的延长线于点H,连接OH交DC于点G,连接HC.下列结论:①OH∥BF;②∠CHF=45°;③;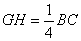
④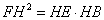.其中正确结论的序号为(    )

①易证得△BCE≌△DCF，
∴∠EBC=∠FDC=22.5°，∠BEC=∠F=67.5°，
∴∠EBC+∠F=90°，
∴BH⊥DF．
又∵BE平分∠DBC，
∴△DBF为等腰三角形，DH=FH，即点H为DF的中点．
∵点O为BD的中点，
∴OH为△DBF的中位线，OH∥BF．
故结论①正确．
②由①可知CH为Rt△DCF的斜边中线，
∴CH=FH，
∴∠HCF=∠F=67.5°，
∴∠CHF=180°-67.5°-67.5°=45°．
故结论②正确．
③由题意可知，，
而点E不是CD的中点，
即，故．
故结论③错误．
④由题意，得
∠FDC=∠EBC=∠DBH，∠BHD=∠DHE=90°，
∴△HDE∽△HBD，
∴，即．
又∵FH=HD，
∴．
故结论④正确．
故选C．

略