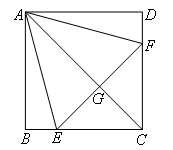
如图,正方形ABCD中,点E,F分别在BC,CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤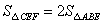.其中正确的有(    )

在正方形ABCD中，，∠B=∠D=90°，
∵△AEF是等边三角形，
∴AE=AF，
∴△ABE≌△ADF，
∴BE=DF，∠DAF=∠BAE=15°．故结论①和②都正确．
∵BC=CD，BE=DF，
∴EC=CF．
∵AE=AF，
∴AC垂直平分EF．故结论③正确．
在Rt△ABE中，易知，
∵EF=AE，DF=BE，
∴．故结论④错误．
经分析可知△EGC≌△FGC，且两个三角形都为等腰直角三角形，
设CG=GE=a，
则AE=2a，．
由勾股定理可得，
∴，
则，
∴，
∴．
而，
∴，则，故结论⑤正确．

略