平面直角坐标系中，□ABOC如图放置，点A、C的坐标分别为（0,3）、（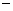
1,0），将此平行四边形绕点O顺时针旋转90°，得到□
．抛物线过点C，A，A′，点M是第一象限内抛物线上的一动点，问：点M在何处时△AMA′的面积最大？最大面积是多少？并求出此时点M的坐标.
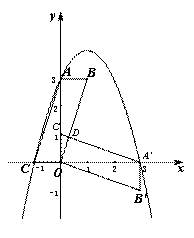
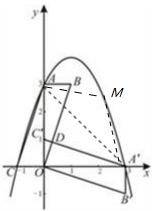
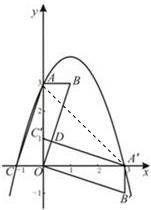
1,0），将此平行四边形绕点O顺时针旋转90°，得到□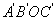
．抛物线过点C，A，A′，点M是第一象限内抛物线上的一动点，问：点M在何处时△AMA′的面积最大？最大面积是多少？并求出此时点M的坐标.
答案
解：∵□ABOC绕点O顺时针旋转90°，得到□A'B'OC'，点A的坐标为（0，3），
∴点A′的坐标为（3，0）．
∴抛物线过点A、C、A′．
设抛物线的函数表达式为y=ax2+bx（a≠0），
可得
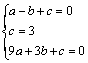，解得
．
故此抛物线的解析式为y=-x2+2x+3．
连接A′A设AA′的函数表达式为y=kx+b，可得
解得
，
AA′的函数解析式是y=-x+3．
设M（x，-x2+2x+3），
S△AMA'=
×3×[-x2+2x+3-（-x+3）]=
，
∵x=
时△AMA'的面积最大S△AMA'=
，
∴M（，
）．
知识点：二次函数综合题
根据旋转的性质求出点A′的坐标，再用待定系数法求出抛物线的解析式；根据垂线长×水平宽度的一半=△AMA＇的面积，即可得到△AMA＇的最大面积和M的坐标．
面积的表达方法不熟练。
WORD格式（
