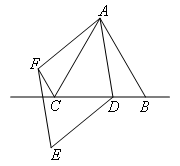
已知△ABC为等边三角形,点D为直线BC上一动点(不与点B,C重合),以AD为边作菱形ADEF(A,D,E,F按顺时针排列),使∠DAF=60°,连接CF.
(1)如图,当点D在边BC上时,容易证明AC=CF+CD,在证明过程中需要用到某对三角形全等,则证明全等时用到的条件是(    )

• A.AAS
• B.ASA
• C.SAS
• D.SSS

答案

正确答案：C

知识点：全等三角形的判定  菱形的性质  类比探究问题  

要证明AC＝CF＋CD，也就是证明BC＝CF＋CD，
而BC＝BD＋CD，所以只需要证明BD=CF．
BD，CF分别在△ADB和△AFC中，考虑证明△ADB和△AFC全等．
∵∠BAC=60°，∠DAF=60°，
∴∠BAD=60°-∠DAC=∠CAF．
又∵AB=AC，AD=AF，
∴△ADB≌△AFC（SAS），
即证明三角形全等时用到的条件是SAS．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>