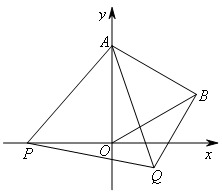
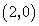如图，在平面直角坐标系中，已知点A（0，2），点P是x轴上一动点，以线段AP为一边，在其一侧作等边三角形APQ．当点P运动到原点O处时，记点Q的位置为B，则当点P从运动到时，点Q运动的路径长为(    )

点Q随着点P的运动而运动，在整个运动过程中，只有点O，A，B三点是固定的，需要发掘点Q与它们之间的联系．
△AOB和△APQ都是等边三角形，并且共用一个顶点，则可能出现全等．
∵∠OAP=∠BAQ=60°-∠OAQ，
AQ=AP，AB=AO，
∴△OAP≌△BAQ，
∴OP=BQ，∠AOP=∠ABQ=90°，
即BQ⊥AB．
∴点Q始终在AB的垂线（过点B）上，且BQ=OP，
∴点Q运动的路径长等于点P运动的路径长，等于4．

略