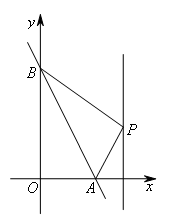
如图,直线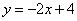 与x轴、y轴分别交于点A,B,点P是第一象限内直线x=3上的一个动点,连接PA,PB,当△PAB为直角三角形时,点P的坐标为( )
与x轴、y轴分别交于点A,B,点P是第一象限内直线x=3上的一个动点,连接PA,PB,当△PAB为直角三角形时,点P的坐标为( )
- A.
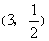 ,
,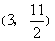
- B.
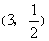 ,
,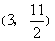 ,
,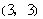
- C.
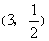 ,
,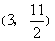 ,
,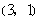 ,
,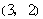
- D.
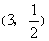 ,
,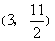 ,
,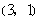 ,
,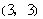
答案
正确答案:D
知识点:一次函数中的存在性问题 直角三角形的存在性
当△PAB为直角三角形时,由于直角顶点未知,所以需要分类讨论.
由题意知,B(0,4),A(2,0).
①当∠BAP=90°时,如图所示,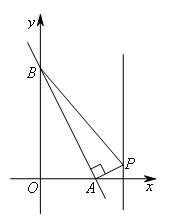
设直线AP的解析式为![]() ,
,
∵PA⊥AB,
∴![]() ,
,
∴![]() .
.
∵点A(2,0)在直线![]() 上,
上,
∴![]() ,
,
∴直线AP的解析式为![]() ,
,
∴点![]() .
.
②当∠ABP=90°时,如图所示,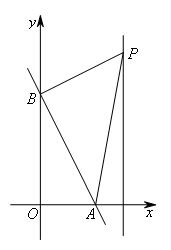
类比①,可求得点![]() .
.
③当∠APB=90°时,如图所示,设直线x=3与x轴交于点N,过点B作BM⊥PN于点M.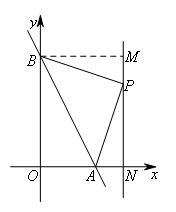
∵∠BPA=90°,容易证明△BMP∽△PNA,
∴![]() .
.
设PN=x,则PM=4-x,
则![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴点P的坐标为![]() .
.
综上所述,点P的坐标为![]() ,
,![]() ,
,![]() ,
,![]() .
.
略








