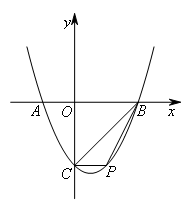
如图,抛物线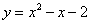 与x轴交于A,B两点,与y轴交于点C,P为抛物线上一点,且点P的横坐标为1,Q是抛物线上异于点P的一点,且
与x轴交于A,B两点,与y轴交于点C,P为抛物线上一点,且点P的横坐标为1,Q是抛物线上异于点P的一点,且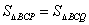 ,则点Q的坐标为( )
,则点Q的坐标为( )
- A.

- B.

- C.

- D.
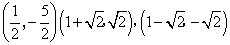
答案
正确答案:C
知识点:二次函数背景下的面积问题 坐标系中的面积问题 平行线转化求面积
经分析可知:A(-1,0),B(2,0),C(0,-2),P(1,-2),
∴直线BC:![]() .
.
△BCP和△BCQ有公共边BC,所以利用平行来转化面积进行计算.
①如图,过点P作![]() ∥BC,交抛物线于点
∥BC,交抛物线于点![]() ,
,
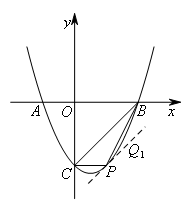
设直线![]() ,
,
∵![]() 在
在![]() 上,
上,
∴![]() ,
,
∴直线![]() .
.
联立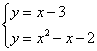 ,解得
,解得![]() ,
,
∴此时点![]() 与点P重合,不符合题意,舍去.
与点P重合,不符合题意,舍去.
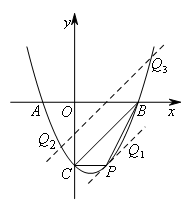
②直线![]() 是由直线BC向下平移1个单位得到的,
是由直线BC向下平移1个单位得到的,
将直线BC向上平移1个单位,得到直线![]() ,如图所示,
,如图所示,
联立 ,解得
,解得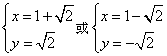 ,
,
∴![]() .
.
综上所述,符合题意的点Q的坐标为![]() .
.
略








