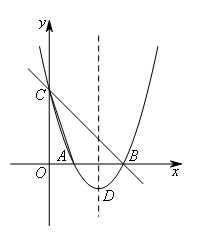
如图,抛物线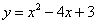 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.抛物线的顶点为D,若在抛物线的对称轴上存在点P使得∠APD=∠ACB,则点P的坐标为( )
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.抛物线的顶点为D,若在抛物线的对称轴上存在点P使得∠APD=∠ACB,则点P的坐标为( )
- A.(2,2)
- B.(1,2)或(1,-2)
- C.
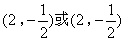
- D.(2,2)或(2,-2)
答案
正确答案:D
知识点:二次函数背景下的存在性问题
从定点开始分析,点A,C,B都是定点,∠ACB是固定的,首先要研究清楚∠ACB,
再去和∠APD对应.
根据二次函数表达式![]() 得A(1,0),B(3,0),
得A(1,0),B(3,0),
C(0,3),D(2,-1),
AB=2,OB=OC=3,![]() ,∠OBC=∠OCB=45°.
,∠OBC=∠OCB=45°.
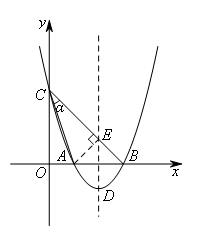
如图,设∠ACB=![]() ,过点A作AE⊥BC于点E,
,过点A作AE⊥BC于点E,
则![]() ,
,
∴![]() .
.
在Rt△ACE中,![]() .
.
接下来需要把∠APD放在一个直角三角形中,使得∠APD的对边和邻边之比为![]() .
.
如图,记对称轴与x轴的交点为F,点![]() 为x轴上方的抛物线对称轴上一点,
为x轴上方的抛物线对称轴上一点,
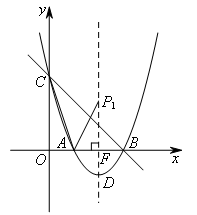
此时![]() ⊥AF,
⊥AF,![]() ,把
,把![]() 放在
放在![]() 中,
中,
要使得![]() ,则需
,则需![]() ,
,
即![]() ,故
,故![]() ,
,
点![]() 的坐标为(2,2).
的坐标为(2,2).
若点![]() 为x轴下方的抛物线对称轴上一点,要使得
为x轴下方的抛物线对称轴上一点,要使得![]() ,
,
利用对称性可求得点![]() 的坐标为(2,-2).
的坐标为(2,-2).
综上得,点P的坐标为(2,2)或(2,-2).
略








