如图,抛物线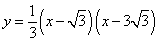 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是抛物线的对称轴
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点D是抛物线的对称轴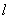 与x轴的交点,点P是抛物线上一点,且∠DCP=30°,则符合题意的点P的坐标为( )
与x轴的交点,点P是抛物线上一点,且∠DCP=30°,则符合题意的点P的坐标为( )
- A.
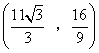 或
或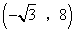
- B.
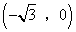 或
或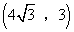
- C.
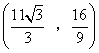
- D.
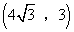
答案
正确答案:C
知识点:三等角模型 二次函数背景下的存在性问题
由题意得,C(0,3),![]() ,
,![]() ,
,![]() .
.
我们知道30°角所对的直角边等于斜边的一半,
也即是含30°角的直角三角形的三边之比是![]() ,
,
要使∠DCP=30°,接下来就需要将∠DCP放到直角三角形中来处理,
而这个直角三角形是通过定点D向定直线DC作垂线得到的.
①先考虑在直线CD上方点P的位置,如图所示,
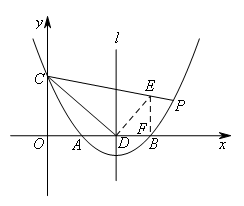
过点D作DE⊥CD交直线CP于点E,过点E作EF⊥x轴于点F,
∵∠DCP=30°,
∴![]() ,
,
由三等角模型易知△DCO∽△EDF,
∴![]() .
.
∵OC=3,![]() ,
,
∴![]() ,EF=2,
,EF=2,
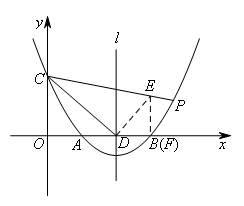
∴![]() ,此时点B和点F重合,标准图如下图所示,
,此时点B和点F重合,标准图如下图所示,
∴直线CE:![]() .
.
联立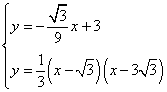 ,解得
,解得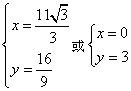 ,
,
∴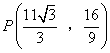 .
.
②考虑直线CD下方点P的位置,
借鉴①中的分析,当∠DCP=30°时,记直线CP为直线m.
如图,过点D作DG⊥CD交直线m于点G,过点G作![]() 于点H,
于点H,
过点C作![]() 于点M,
于点M,
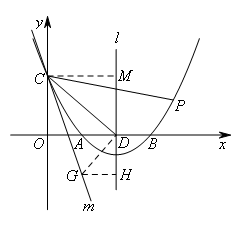
易知△MCD∽△HDG,且相似比为![]() .
.
∵![]() ,DM=3,
,DM=3,
∴DH=2,![]() ,
,
∴![]() ,
,
∴直线CG:![]() ,
,
联立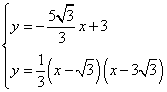 ,解得
,解得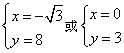 .
.
∵![]() 在第二象限,观察图形可知,此时∠DCP=150°,不符合题意.
在第二象限,观察图形可知,此时∠DCP=150°,不符合题意.
∴符合题意的点P的坐标为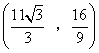 .
.
略








