如图,二次函数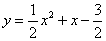 的图象与x轴交于A,B两点(点A在点B的左侧),
的图象与x轴交于A,B两点(点A在点B的左侧),
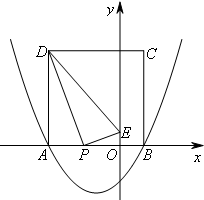
以AB为边在x轴上方作正方形ABCD,P是x轴上的一动点(不与点A重合),连接DP,过点P作PE⊥DP交y轴于点E.当△PED是等腰三角形时,点P的横坐标为( )
- A.-4
- B.-3
- C.-3或-4
- D.-4或4
答案
正确答案:D
∵![]() ,
,
∴A(-3,0),B(1,0).
∵四边形ABCD是正方形,
∴D(-3,4).
△PED中,D为定点,P,E为动点,且始终保持∠DPE=90°,
若要使△PED是等腰三角形,只能是DP=PE(此时△PED是等腰直角三角形),
但是需要根据点P位置的不同进行分类.
设点P的横坐标为t![]() .
.
①当![]() 时,如图所示,
时,如图所示,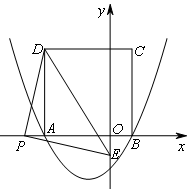
∵∠DPE=∠DAP=∠POE=90°,DP=PE,
易证△DAP≌△POE,
∴OP=AD=4,
∴![]() .
.
②当![]() 时,如图所示,
时,如图所示,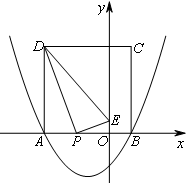
∵∠DPE=∠DAP=∠POE=90°,DP=PE,
易证△DAP≌△POE,
∴OP=AD=4,
∴![]() (不符合要求,舍).
(不符合要求,舍).
③当![]() 时,如图所示,
时,如图所示,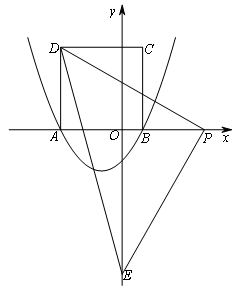
∵∠DPE=∠DAP=∠POE=90°,DP=PE,
易证△DAP≌△POE,
∴OP=AD=4,
∴![]() .
.
综上,符合题意的点P的横坐标为-4或4.
略








