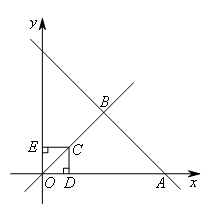
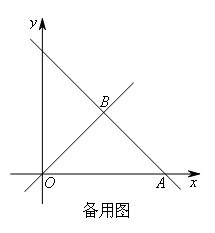
如图，直线y=-x+4与x轴交于点A，与直线y=x交于点B．动点D从原点O出发，以每秒2个单位长度的速度沿OA向终点A运动（点D不与点O，A重合），过点D作DC⊥x轴，交线段OB或线段BA于点C，过点C作CE⊥y轴于点E．设运动t秒时，矩形ODCE与△OAB重叠部分的面积为S，则S与t之间的函数关系式为(    )

• A.
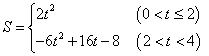
• B.
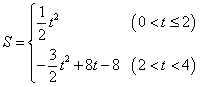
• C.
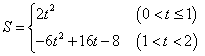
• D.

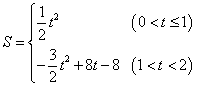
答案

正确答案：C

知识点：一次函数之动点问题  

由直线y=x知，∠AOB=45°，
由直线y=-x+4知，∠OAB=45°，OA=4，
．
如图，过点B作BM⊥x轴于点M，则OM=BM=2．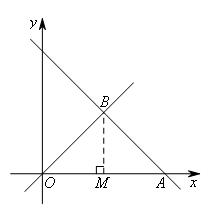

研究动点的运动情况，确定运动的时间范围为．
①当时，如图，

∵OD=2t，则CD=2t，
∴．
②当时，画出符合题意的图形，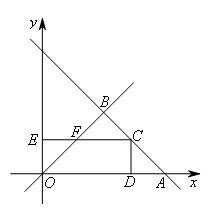

∵OD=2t，则AD=4-2t，
∴CD=4-2t，，
∴，
∴CF=4t-4，
∴．
综上，答案选C．

略

下载次数：0

WORD格式（含答案版下载 无答案版下载）

<<上一题   下一题>>