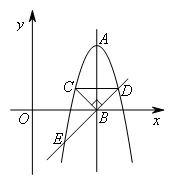
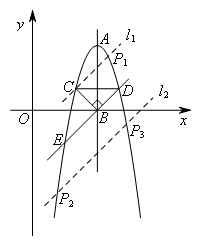
（上接第1题）（2）延长DB交抛物线于点E，若抛物线上存在点P，使得△DEP的面积与△DEC的面积相等，则点P的坐标为( )
- A.
，
，
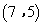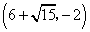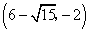
- B.，
，
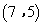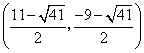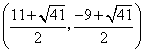
- C.，
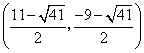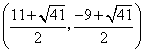
- D.，
，
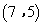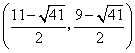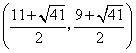
答案
正确答案：B
由（1）中的分析易得，D（8，2），B（6，0），
∴直线DE：y=x-6．
△DEP与△DEC中，只有点P是动点，并且两个三角形有公共边DE，
以DE为底来考虑，只需要保证高相等即可．
①过点C作直线
∥DE交抛物线于点
，如图所示，
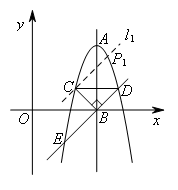
设：
，
把C（4，2）代入，解得
，
∴：
．
联立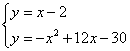
，解得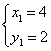
，
，
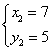故
．
②直线是由直线DE向上平移4个单位得到的，
将直线DE向下平移4个单位可以得到直线
，
直线
与抛物线的交点
也满足题意，如图所示，
联立
，
解得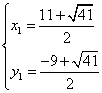
，
，
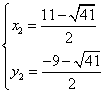故
，
．
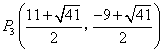综上，符合条件的点P的坐标为
，
，
．
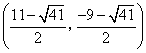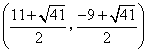略
WORD格式（
