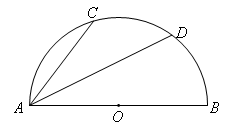
如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,交半圆O于点D,则AD的长为( )
- A.
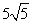 cm
cm - B.
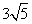 cm
cm - C.4cm
- D.
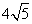 cm
cm
答案
正确答案:D
知识点:垂径定理 圆周角定理 相似三角形的性质和判定
方法一:如图,连接OD,OC,作DE⊥AB于点E,OF⊥AC于点F.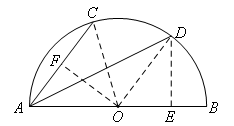
∵∠CAD=∠BAD,
∴∠DOB =2∠BAD=∠OAC,
∴△AOF≌△ODE,
∴OE=AF=![]() AC=3cm.
AC=3cm.
在Rt△DOE中,DE=4cm,
在Rt△ADE中,AD=![]() cm.
cm.
方法二:由直径想到圆周角,进而连接BC,BD,OD,
如图,设线段CB与AD交于点E,与OD交于点F.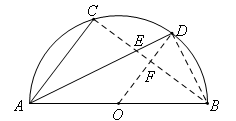
容易证明,在Rt△ABC中,BC=8cm,OD∥AC,
∴点F是BC的中点,OF是△BCA的中位线,
∴OF=3cm,BF=CF=![]() .
.
∵△DFE∽△ACE,且DF=2cm,AC=6cm,
∴![]() ,则EF=1cm,CE=3cm,
,则EF=1cm,CE=3cm,
∴CE:AC=1:2.
∵△CAE∽△DAB,
∴DB:AD=1:2.
在Rt△DAB中,由勾股定理可以得到AD=![]() cm.
cm.
方法三:还记得可以用相似来证明的“三角形一个角的平分线分对边所成的两条线段与这个角的两邻边对应成比例”这个定理吗?这个题目也可以借助于这个来做(有兴趣的同学可以尝试一下,连接BC,BD).
略








