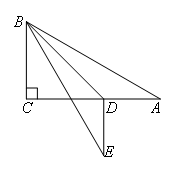
如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=1,点D在AC上,将△ADB沿直线BD翻折后,点A落在点E处.如果AD⊥DE,那么线段DE的长为( )
- A.1
- B.
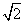
- C.
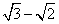
- D.
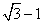
答案
正确答案:D
知识点:含特殊角(15°的倍数)的三角形 翻折变换(折叠问题)
研究基本图形可以知道△ABC的三边长,
由折叠可知DE=AD,要求DE的长也就转化为求AD的长,
那么只需要找到DC的长即可,这个时候就需要借助折叠产生的条件进行分析.
由折叠可知,△BDE≌△BDA,
∴DE=AD,∠BDE=∠BDA.
∵AD⊥DE,
∴∠EDA=∠EDC=90°,
∴∠BDE=∠BDA=135°,
∴∠BDC=45°,
∴△BDC是等腰直角三角形,
∴BC=CD=1.
由题意得,![]() ,
,
∴![]() ,
,
∴![]() .
.
略








