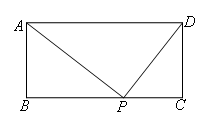
如图,矩形ABCD中,AD=a,AB=b,若在BC边上至少存在一点P,使△ABP,△APD,
△PCD两两相似,则a,b之间的关系一定满足( )
- A.
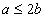
- B.
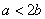
- C.
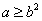
- D.
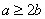
答案
正确答案:D
知识点:相似三角形的判定与性质 相似三角形的存在性
1.解题要点
①对要研究的3个三角形进行分析,△ABP和△PCD都是直角三角形,
若3个三角形两两相似,则△APD为直角三角形,
结合图形可知,只能是∠APD=90°;
②当∠APD=90°时,调用“三等角模型”,能够得到△ABP∽△PCD∽△DPA;
③相似能够得到比例关系,根据第一组相似能够得到![]() .
.
若存在一点P满足题意,设PC=x,则根据相似建立的关于x的方程应该有解(将存在性问题转化为方程有解的问题).
2.解题过程
∵△ABP,△APD,△PCD两两相似,△ABP和△PCD都是直角三角形,
∴∠APD=90°,
∴△ABP∽△PCD∽△DPA,
∴![]() .
.
设PC=x,则![]() ,
,
∴![]() ,整理可得
,整理可得![]() .
.
若存在点P满足题干要求,则一元二次方程![]() 有正实数根,
有正实数根,
由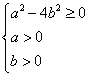 ,得
,得![]() .
.
又∵![]() ,
,![]() ,
,
∴一元二次方程![]() 在
在![]() 的前提下的解均为正数.
的前提下的解均为正数.
综上得,a,b之间的关系一定满足![]() .
.
略








