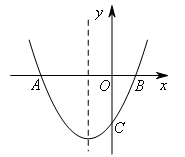
如图,已知抛物线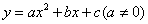 的对称轴为直线x=-1,抛物线与x轴交于A,B两点,与y轴交于点C,其中A(-3,0),C(0,-2).若在对称轴上存在一点P,使得△PBC的周长最小,则点P的坐标为( )
的对称轴为直线x=-1,抛物线与x轴交于A,B两点,与y轴交于点C,其中A(-3,0),C(0,-2).若在对称轴上存在一点P,使得△PBC的周长最小,则点P的坐标为( )
- A.(-1,-2)
- B.(-1,-4)
- C.
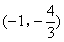
- D.
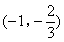
答案
正确答案:C
知识点:二次函数与几何综合 轴对称——线段之和最小
1.解题要点
①△PBC的周长为PC+PB+BC,BC长度固定,要求周长的最小值,需先求PC+PB的最小值.
②观察题目特征,B,C为定点,P为对称轴上的动点,点B,C在对称轴的同侧.
要求PC+PB的最小值,调用轴对称最值模型,作其中一定点关于对称轴的对称点,利用两点之间线段最短解决问题.
2.解题过程
由题意得,点A和点B关于对称轴对称.
如图,连接AC,与对称轴的交点即为PC+PB最小时对应的点P.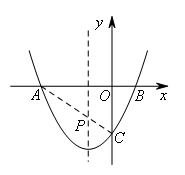
∵A(-3,0),C(0,-2),
∴直线AC:![]() .
.
∵点P的横坐标为-1,
∴![]() .
.
略








