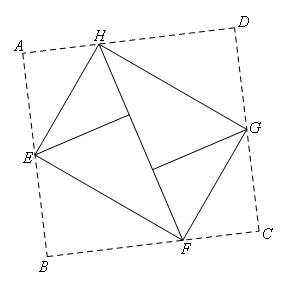
如图，将矩形ABCD的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形EFGH．
若EH=3，EF=4，则边AD的长为____．

如图，由折叠性质知，∠1=∠2，∠3=∠4．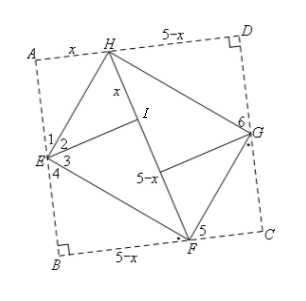

则∠2+∠3=90°，即∠HEF=90°，
同理∠EFG=∠FGH=90°，
则四边形EFGH是矩形，则HG=EF．
又EH=3，EF=4，由勾股定理得，HF=5．
设AH=x，则HI=AH=x，IF=BF=5-x．
由∠B=∠D=90°，通过导角可得∠4=∠5=∠6，
则△BEF≌△DGH（AAS），BF=DH，
则AD=AH+DH=x+5-x=5．
即AD的长为5．

略